What are the components of the vector between the origin and the polar coordinate (3, (13pi)/12)?
1 Answer
Mar 14, 2018
Coordinates are
Explanation:
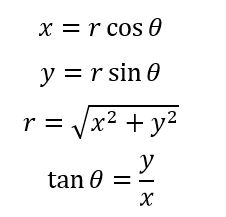
Given :
Slope
Coordinates are
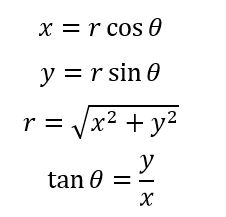
Given :
Slope