Component Vectors
Key Questions
-
Answer:
#" "#
Please read the explanation.Explanation:
#" "#
How do we use the components of two vectors to find the resultant vector by adding the two vectors ?A Vector is defined as a quantity with both magnitude and direction.
Two vectors are shown below:
#color(red)(vec(OA) and vec(OB)# We will also be using these vectors in our example later.
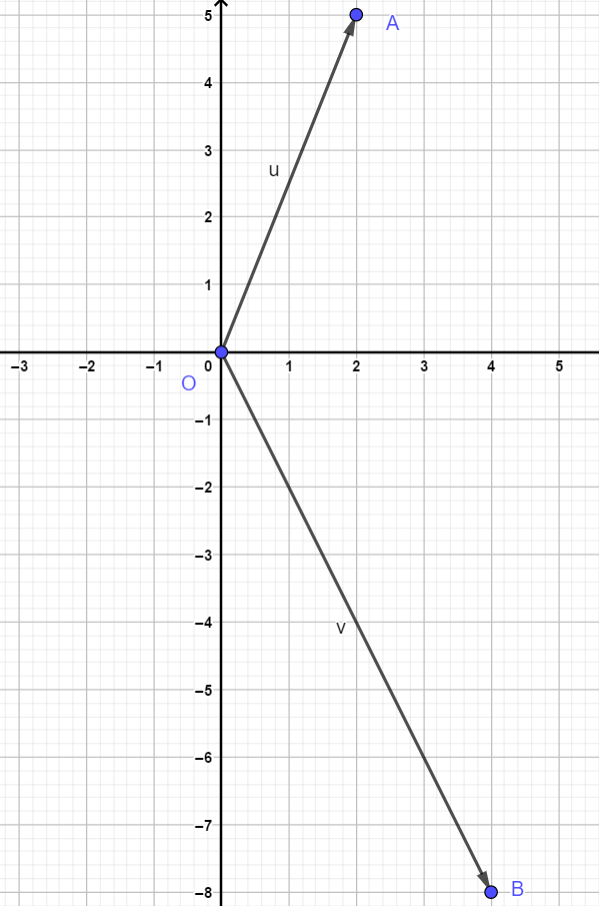
#vec(OA) = hat(u)=(2 hat i+5 hat j)# In component form
#hat(u)=<2,5># #vec(OB) = hat(v)=(4 hat i-8 hat j)# In component form
#hat(v)=<4,-8># Let us see how we can add these two vectors:
#hat (u) + hat (v) = (2 hat i+5 hat j)+(4 hat i-8 hat j)# Using component form:
#hat (u) + hat (v) = <2 ,5 >+<4-8 ># Add
#color(red)(i# components and#color(red)(j# components together:#hat (u) + hat (v) = <2+4>+<5-8 ># #color(red)(hat (u) + hat (v) =<6, -3># We can represent this solution graphically as follows:
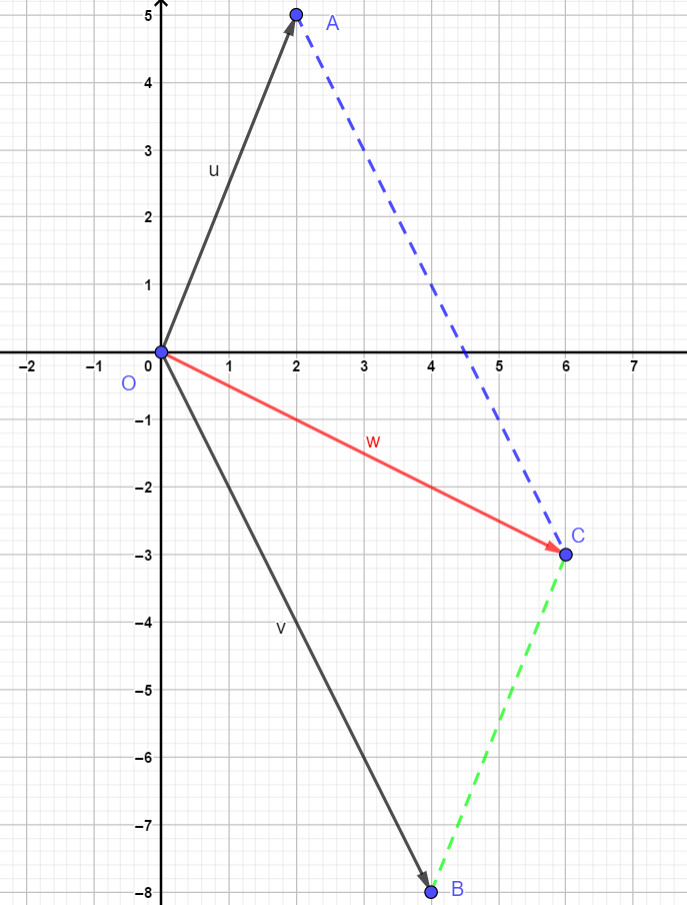
The solution is represented by
#color(red)(w=hat (u) + hat (v) =<6, -3># OR
#color(red)(w=hat (u) + hat (v) =(6i -3j)# Note: Alternative graphical solution process:
#vec(OA)# can also be translated to the line in green (BC).OR
#vec(OB)# can be translated to the line in blue (AC).We can see that
#color(red)(w# is the solution.Hope it helps.
-
To find the magnitude of a vector using its components you use Pitagora´s Theorem.
Consider in 2 dimensions a vector
#vecv# given as:
#vecv = 5veci + 3vecj# (where#veci# and#vecj# are the unit vectors on the x and y axes)
The magnitude of this vector (or its length in geometrical sense) is given using Pitagora's Theorem, as:
#|vecv| =sqrt(5^2+3^2)= 5,8# The same thing applies in 3 dimensions, the only thing is to include the third component.
So if the vector is now given as:
#vecv = 5veci+ 3vecj + 2veck#
The magnitude will be:
#|vecv|= sqrt(5^2+3^2+2^2) = 6,2# -
Often when two processes interact we only know the component vector values and need to be able to combine these to get a desired result.
This might be more easily understood by an example:
Suppose I am trying to fly from point A to point B which is due North of point A. My plane flies at an air speed of 100 miles/hour but there is a wind blowing due West at 30 miles/hour. How many degrees East of North do I need to orient my plane to fly in a straight line to B?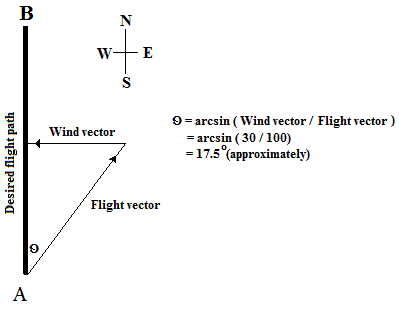
From the above diagram, I need to head my plane (approximately)
#17.5^o# East of North.This problem could be extended to ask:
If it is 200 miles from A to B and my plane has enough gas to fly 250 miles will I be able to make this trip? -
A vector has both magnitude (which is its length) and direction (which is its angle).
Any two dimentional vector at an angle will have a horizontal and a vertical component .
A vector written as ( 12 , 8 ) will have 12 as its horizontal component, and 8 as its vertical component, and because both components are positive, the vector is pointing to the northeastern direction.