Question

What are the components of the vector between the origin and the polar coordinate `(3, (19pi)/12)`?

Answer 1

see Details below.

Explanation:

`Given r = 3, theta = (19pi)/12`

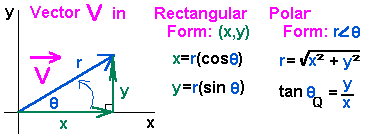
To find components of the vector between origin and the given point (3,(19pi)/12#

`theta =( (19pi)/12)^c = 285^@`

`x = r cos theta = 3 * cos ((19pi)/12) = 0.7765`

`y = r sin theta = 3 * sin ((19pi)/12) = -2.8978`

`tan theta = tan ((19pi)/12) = y / x = - 2.8978 / 0.7765 = -3.7321`

In rectangular form `(x,y) = (0.7765, -2.8978)`

In polar form `(r, theta) = (3, (19pi)/12)`

Slope of the vector m = tan theta = - 3.7321#

Vector is in the IV quadrant.