What are the set of four quantum numbers that represent the electron gained to form the #Br# ion from #Br# atom?
1 Answer
Explanation:
As you know, there are four quantum numbers used to describe the position and spin of an electron in an atom.
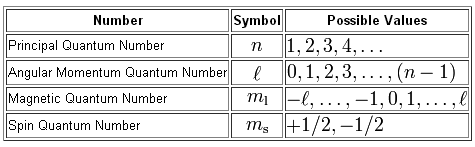
Your goal here will be to use the information provided by the electron configuration of a neutral bromine atom,
So, bromine is located in period 4, group 17 of the periodic table and has an atomic number equal to
The electron configuration of a neutral bromine atom looks like this
#"Br: " 1s^2 2s^2 2p^6 3s^2 3p^6 3d^10 color(red)(4) s^2 color(red)(4)p^5#
Notice that bromine's outermost electrons, i.e. its valence electrons, are located on the fourth energy level,
The incoming electron will be added to this energy level, so right from the start you know that it must have
The angular momentum quantum number,
The magnetic quantum number,
#4p_x -> m_l = -1# #4p_y -> m_l = +1# #4p_z -> m_l = color(white)(-)0#
This is used by convention because the wave function associated with
Since the neutral bromine atom already has 5 electrons in its 4p-subshell, you can say that its
The incoming electron will thus be added to the half-empty
Finally, the spin quantum number,
The quantum number set that describes the incoming electron will thus be
#color(green)(|bar(ul(color(white)(a/a)color(black)(n = color(red)(4), l = 1, m_l = 0, m_s = -1/2)color(white)(a/a)|)))#
SIDE NOTE You'll sometimes see this notation used for the magnetic quantum number
#4p_x -> m_l = -1# #4p_y -> m_l = color(white)(-)0# #4p_z -> m_l = +1#
You can use this if you want, but make sure that you are consistent.
In this notation, the wave function associated with

