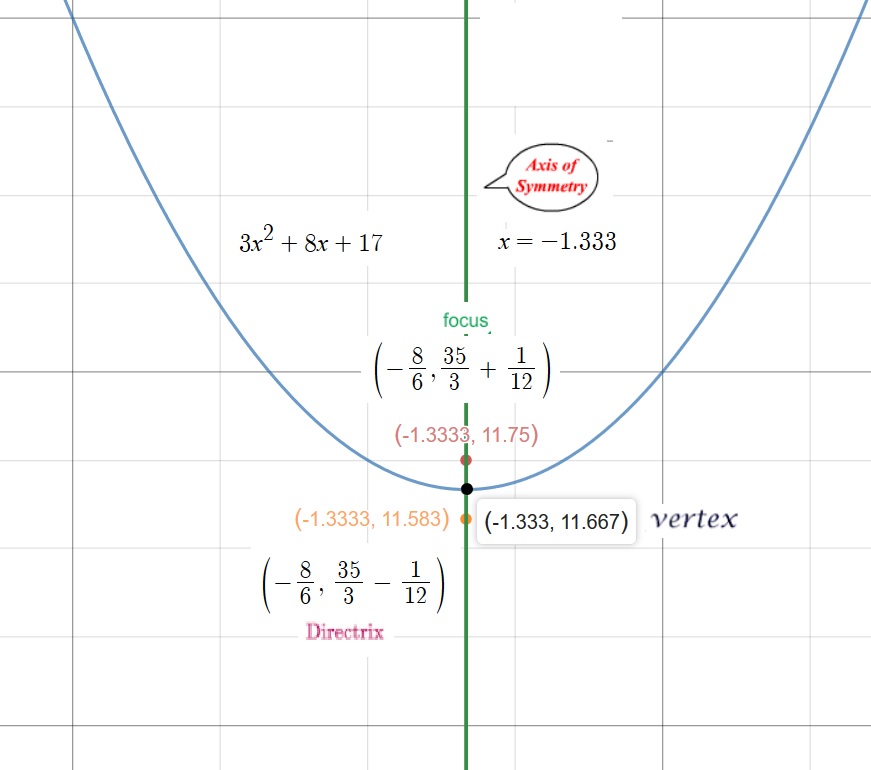
What are the vertex, focus and directrix of # y=3x^2+8x+17 #?
1 Answer
Vertex
Focus
Directrix
Labelled Graph is also available
Explanation:
We are given the quadratic
Coefficient of the
Hence, our Parabola Opens Up and we will also have a Vertical Axis of Symmetry
We need bring our quadratic function to the form given below:
Consider
Note that, we need to keep both the
To find the Vertex, we will Complete the Square on x
Divide every single term by
What value goes into the
Divide the coefficient of the x.term by
The answer goes into the
Factor
We can rewrite to bring it to the required form given below:
whered
Hence, our Vertex will be
Vertex
Using
Hence,
Focus is always on the Axis of Symmetry
Focus is also inside the Parabola
Focus will have the same x.Value as the Vertex because it lies on the Axis of Symmetry
The Axis of Symmetry is at
The Directrix is always Perpendicular to the Axis of Symmetry
The Value of P tells us how far the Focus is from the Vertex
The Value of P also tells us how far the Directrix is from the Vertex
Since we know that
Our Focus is also
Also, Focus is inside our parabola.
So, the Location of the Focus is given by
Focus
Directrix is always Perpendicular to the Axis of Symmetry
Please refer to the graph below:
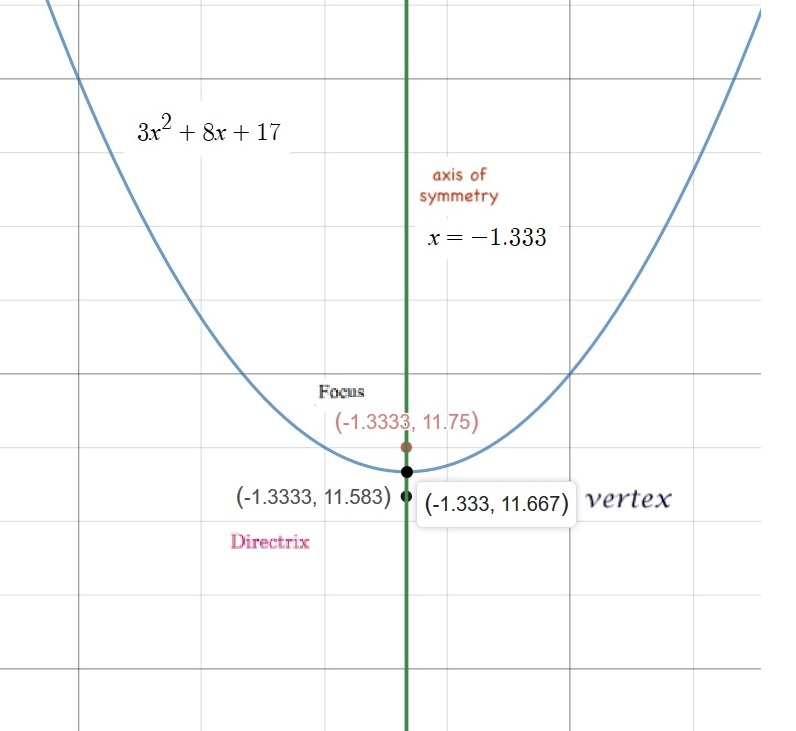
A labelled graph given below with a few intermediate calculations shows on it might also be useful