Question

What are the vertex, focus and directrix of `y=x^2-3x+4`?

Answer 1

`"vertex="(1.5,1.75)`
`"focus="(1.5,2)`
`"directrix: y=1.5`

Explanation:

`y=a(x-h)^2+k " the vertex form of parabola"`

`"vertex="(h,k)`

`"focus="(h,k+1/(4a))`

`y=x^2-3x+4 "your parabola equation"`

`y=x^2-3xcolor(red)(+9/4-9/4)+4`

`y=(x-3/2)^2-9/4+4`

`y=(x-3/2)^2+7/4`

`"vertex"=(h,k)=(3/2,7/4)`

`"vertex="(1.5,1.75)`

`"focus="(h,k+1/(4a))`

`"focus="(1.5,7/4+1/(4*1))=(1.5,8/4)`

`"focus="(1.5,2)`

`"Find directrix :"`

`"take a point(x,y) on parabola"`

`"let " x=0`

`y=0^2-3*0+4`

`y=4`

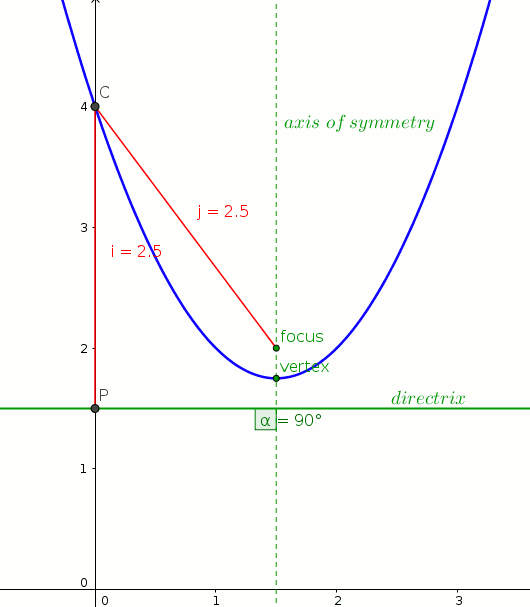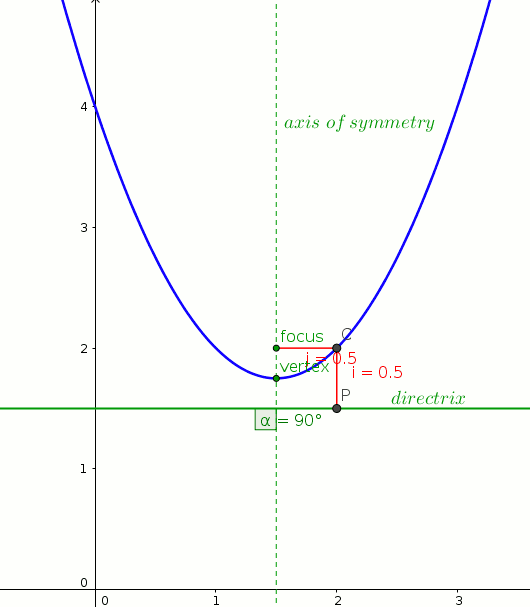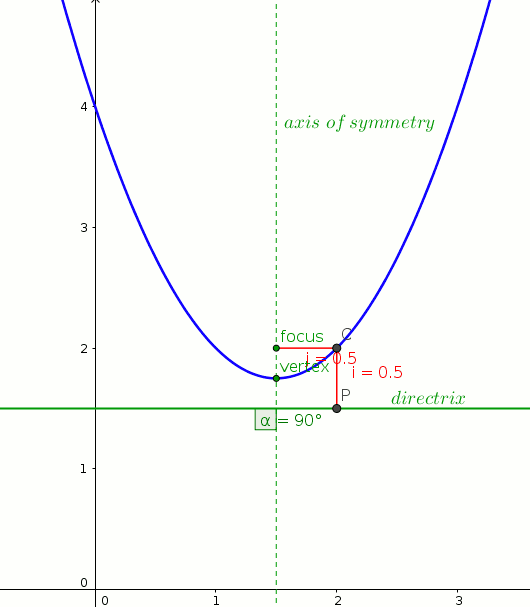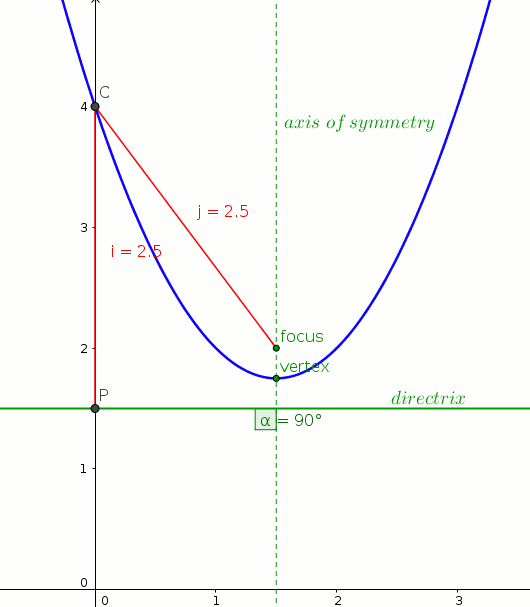
`C=(0,4)`

`"find distance to focus"`

`j=sqrt((1.5-0)^2+(2-4)^2)`

`j=sqrt(2.25+4)`

`j=sqrt(6.25)`

`j=2.5`

`directrix=4-2.5=1.5`

`y=1.5`