Question

What are the vertex, focus and directrix of `y=x^2 – 6x + 5`?

Answer 1

Vertex `(3,-4)`
Focus `(3, -3.75)`
Directrix `y=-4.25`

Explanation:

Given -

`y=x^2-6x+5`

Vertex

`x=(-b)/(2a)=(-(-6))/(2xx1)=6/2=3`

At `x=3`

`y=3^2-6(3)+5=9-18+5=-4`

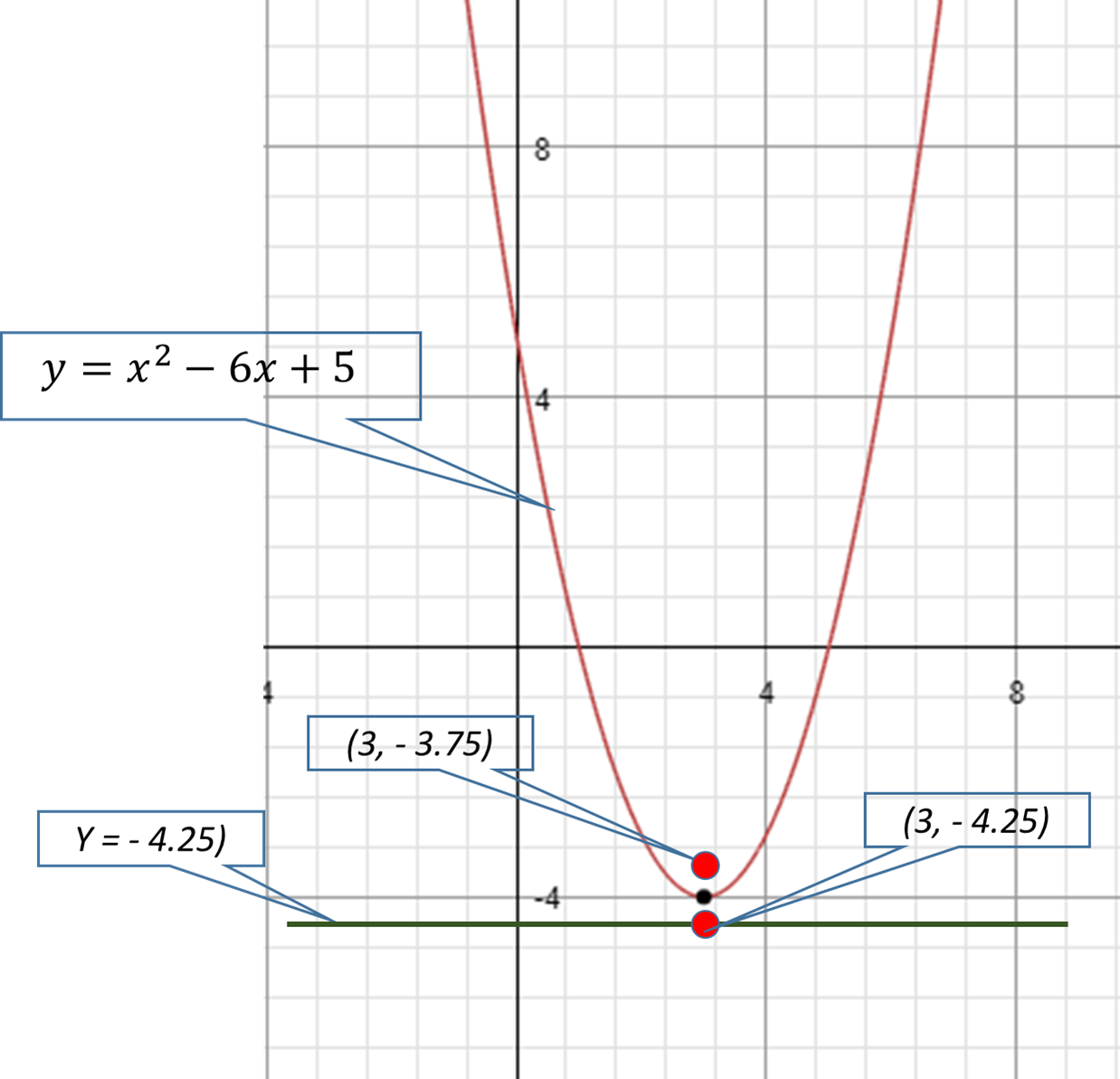
Vertex `(3,-4)`

Focus and Directrix

`x^2-6x+5=y`

Since the equation is going to be in the form or -

`x^2=4ay`

In this equation `a` is focus

the parabola is opening up.

`x^2-6x=y-5`

`x^2 -6x+9=y-5+9`
`(x -3)^2=y+4`

To find the value of `a`, we manipulate the equation as -

`(x-3)^2=4xx 1/4 xx(y+4)`

`4 xx1/4=1` So the manipulation didn't affect the value `(y+4)`

The value of `a=0.25`

Then Focus lies 0.25 distance above vertex

Focus `(3, -3.75)`

Then Directrix lies 0.25 distance below vertex`(3, -4.25)`

Directrix `y=-4.25`