Question

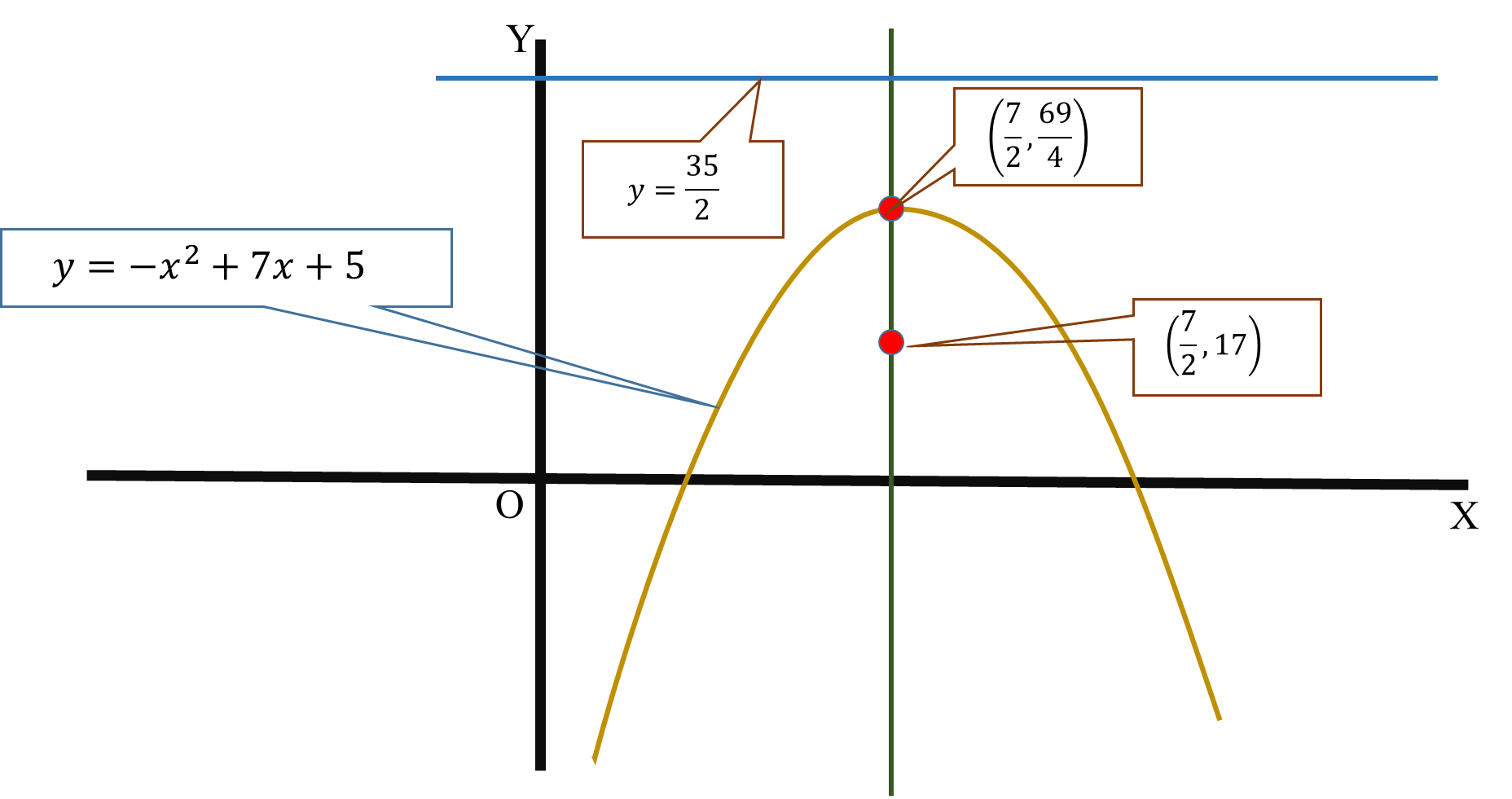
What are the vertex, focus, and directrix of `y=-x^2+7x+5`?

Answer 1

Vertex `(7/2, 69/4)`
Focus `(7/2,17)`
Directrix `y=35/2`

Explanation:

Given -

`y=-x^2+7x+5`

This parabola opens down because it is in the form

`(x-h)^2=-4a(y-k)`

Let us convert the given equation in this form

`-x^2+7x+5=y`
`-x^2+7x=y-5`
`x^2-7x=-y+5`
`x^2-7x+49/4=-y+5+49/4`
`(x-7/2)^2=-y+69/4`
`(x-7/2)^2=-1(y-69/4)`

`(x-7/2)^2=-4 xx 1/4(y-69/4)`
`a=1/4` Distance between focus and vertex and also distance between vertex and directix.

Vertex `(7/2, 69/4)`
Focus `(7/2,17)`
Directrix `y=35/2`