The trick is to evaluate #sin(cot^-1(5))+5sin(tan^-1(2))# is
breaking down the problem and solving each part separately.
Let us start with evaluating #cot^-1(5)#
Let #theta=cot^-1(5)#
Then #cot(theta) = 5#
#cot(theta) = "adjancent"/"opposite"#
If I have to show that in a right triangle.
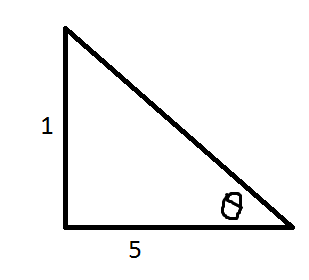
The hypotenuse would be #sqrt(1^2+5^2)#
Hypotenuse #= sqrt(26)#
#sin(theta) = "Opposite"/"hypotenuse"#
#sin(theta) = 1/sqrt(26)#
Rationalizing the denominator we get
#sin(theta) = (sqrt(26))/26#
Remember #theta# was #cot^-1(5))#
#sin(cot^-1(5)) = (sqrt(26))/26#
Now let us work on the second part.
#5sin(tan^-1(2))#
#Theta=tan^-1(2)#
#tan(Theta) = 2#
#tan(Theta) = "Opposite"/"Adjacent"#
Let us put that in a right triangle.
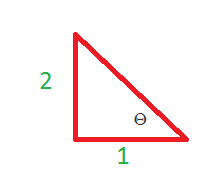
Now to find the hypotenuse
Hypotenuse #=sqrt(2^2+1^2)#
Hypotenuse #=sqrt(5)#
#sin(Theta) = "Opposite"/"hypotenuse"#
#sin(Theta) =2/sqrt(5)#
Rationalizing the denominator
#sin(Theta)=(2sqrt(5))/5#
Remember #Theta=tan^-1(2)#
#sin(tan^-1(2))=(2sqrt(5))/5#
#5sin(tan^-1(2))=5**(2sqrt(5))/5#
#5sin(tan^-1(2))=2sqrt(5)#
Now the final steps
#sin(cot^-1(5))+5sin(tan^-1(2)) = sqrt(26)/26+2sqrt(5)#
#sin(cot^-1(5))+5sin(tan^-1(2)) = (sqrt(26)+52sqrt(5))/26#



