What electron configuration represents an atom in the excited state?
2 Answers
The excited state electron configuration of an atom indicates the promotion of a valence electron to a higher energy state.
Explanation:
An electron configuration representing an atom in the excited state will show a valence electron promoted to a higher energy level.
Example
The ground state electron configuration of sodium is
In its excited state, the valence electron in the
This is a very unstable condition and the excited electron will drop back down to the
The first excited state is the same configuration as the ground state, except for the position of one electron.
As an example, sodium goes through a
The ground state electron configuration for sodium is:
#color(blue)(1s^2 2s^2 2p^6 3s^1)#
And the first excited state electron configuration for sodium is:
#color(blue)(1s^2 2s^2 2p^6 3p^1)#
This corresponds to an excitation to a first excited state that is less stable; that then leads to a relaxation back down to the ground state. The relaxation emits yellow light (
I end up going through selection rules (which help you predict whether an electronic transition is allowed or forbidden), term symbols, and predicting transitions. That overall tells you how I know that a
(If you want, you can skip the term symbols contextual section; it's optional.)
You may or may not have learned selection rules yet, but they aren't too difficult to take note of. They would help you determine how to write electron configurations for excited states.
SELECTION RULES
The selection rules govern how an electron is observed to transition (excite upwards or relax downwards) from one orbital to another.
Formally, they are written as:
#color(blue)(DeltaS = 0)#
#color(blue)(DeltaL = 0, pm1)#
#color(blue)(L + S = J)#
#:. color(blue)(DeltaJ = 0, pm1)# where
#DeltaS# is the change in intrinsic angular momentum of the electron (spin multiplicity is#2S + 1# ),#DeltaL# is the change in orbital angular momentum, and#DeltaJ# is the change in the total angular momentum.
It is helpful to know the selection rules if you want to predict how an excited state configuration can be written just based on the atom's (correct) ground state configuration.
EXAMPLES OF ELECTRONIC EXCITATION TRANSITIONS
Allowed:
An example of an allowed electronic transition upwards of one unpaired electron to an empty orbital:
#color(green)(2s -> 2p)# (#color(green)(DeltaS = 0# ,#color(green)(DeltaL = +1)# ,#color(green)(DeltaJ = 0, pm1)# )
Forbidden:
An example of a forbidden electronic transition upwards of one unpaired electron to an empty orbital:
#color(green)(3s -> 3d)# (#color(green)(DeltaS = 0)# ,#color(green)(DeltaL = color(red)(+2))# ,#color(green)(DeltaJ = 0, pm1, color(red)(pm2))# )
TERM SYMBOLS / CONTEXT
"I've never seen
You can read more about them here:
http://socratic.org/scratchpad/3616fa1583309e7c0ed2
DISCLAIMER: The above link explains term symbols for context. It helps to know this, but you don't have to know this like the back of your hand unless you are taking Physical Chemistry.
APPLICATION OF THE SELECTION RULES
Alright, so let's apply the selection rules themselves. I gave examples already, so let's work off of the allowed transition example and change it a little bit. The values for
Let us examine this energy level diagram for sodium:
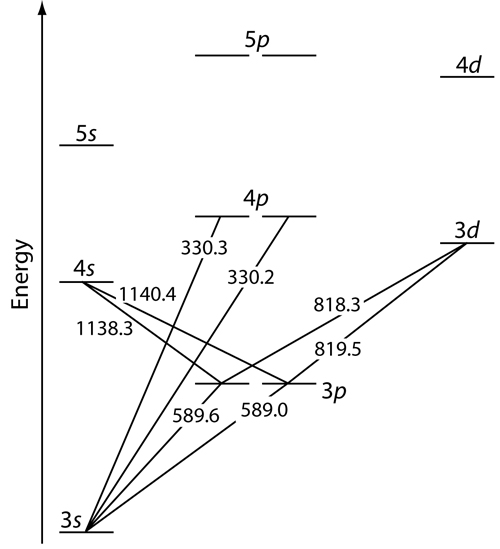
You can see lines on the diagram going from the
These two lines are marked
Therefore, a common excitation/relaxation transition sodium makes is:
Excitation Transition:
#3s -> 3p# (#DeltaS = 0# ,#DeltaL = +1# ,#DeltaJ = 0, +1# )Relaxation Transition:
#3p -> 3s# (#DeltaS = 0# ,#DeltaL = -1# ,#DeltaJ = 0, -1# )(Term symbol notation:
#""^2 S_"1/2" -> ""^2 P_"1/2", ""^2 P_"3/2"# , excitation
#""^2 P_"1/2", ""^2 P_"3/2" -> ""^2 S_"1/2"# , relaxation)
So the ground state electron configuration for sodium is:
#color(blue)(1s^2 2s^2 2p^6 3s^1)#
And the first excited state electron configuration for sodium is:
#color(blue)(1s^2 2s^2 2p^6 3p^1)#
Lastly, an easy way to remember what transitions are allowed is to note that electronic transitions on energy level diagrams are diagonal, and involves adjacent columns.


