Question

What is a first order half life?

Answer 1

See explanation.

Explanation:

The half-life of a chemical reaction, regardless of its order, is simply the time needed for half of an initial concentration of a reactant to be consumed by the reaction.

Now, a first-order reaction is characterized by the fact that the rate of the reaction depends linearly on the concentration of one reactant.

For a first-order reaction

`"A " -> " products"`

the differential rate law allows you to express the rate of the reaction in terms of the change in the concentration of the reactant (or of a product)

`"rate" = -(d["A"])/dt = k * ["A"]`

The integrated rate law, which establishes a relationship between the change in the concentration of the reactant and time, can be obtained by integrating the differential rate law.

The integrated rate law for a first-order reaction looks like this -- mind you, I will not do the derivation here.

`color(blue)(|bar(ul(color(white)(a/a)color(black)(ln["A"] = ln["A"]_0 - k * t)color(white)(a/a)|)))`

Here

`["A"]` - the concentration of reactant `"A"` after a time `t`
`["A"]_0` - the initial concentration of the reactant `["A"]`
`k` - the rate constant of the reaction

So, the half-life of the reaction, `t_"1/2"`, corresponds to the period of time in which the concentration of the reactant goes from `["A"]_0` to `["A"] = ["A"]_0/2`.

You can thus say that

`ln(["A"]_0/2) = ln["A"]_0 - k * t_"1/2"`

This can be rearranged to get

`ln(["A"]_0/2) - ln["A"]_0 = - k * t_"1/2"`

`ln(color(red)(cancel(color(black)(["A"]_0)))/2 * 1/color(red)(cancel(color(black)(["A"]_0)))) = -k * t_"1/2"`

`ln(1/2) = - k * t_"1/2"`

You can rewrite this as

`overbrace(ln(1))^(color(blue)(=0)) - ln(2) = - k * t_"1/2"`

`-ln(2) = -k * t_"1/2"`

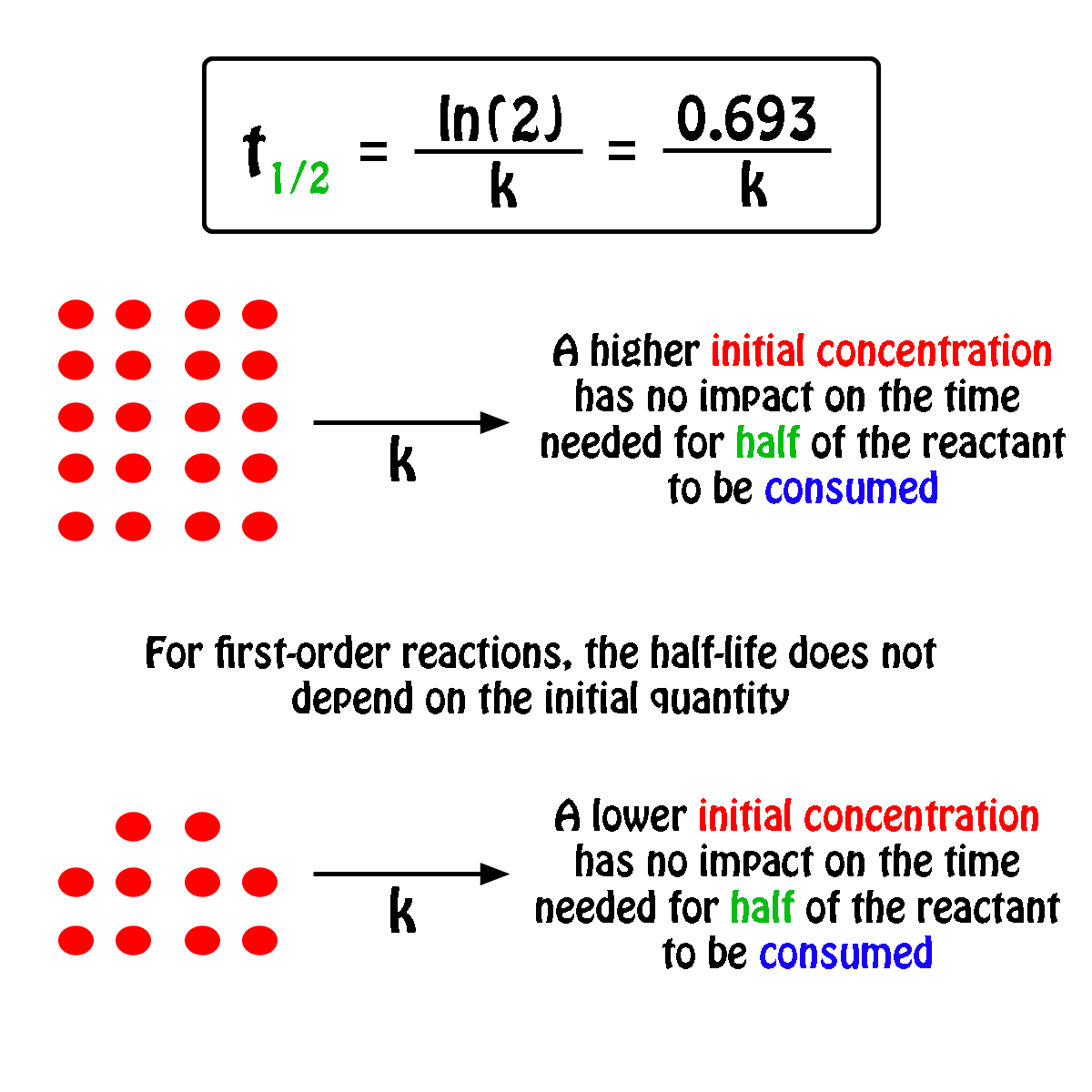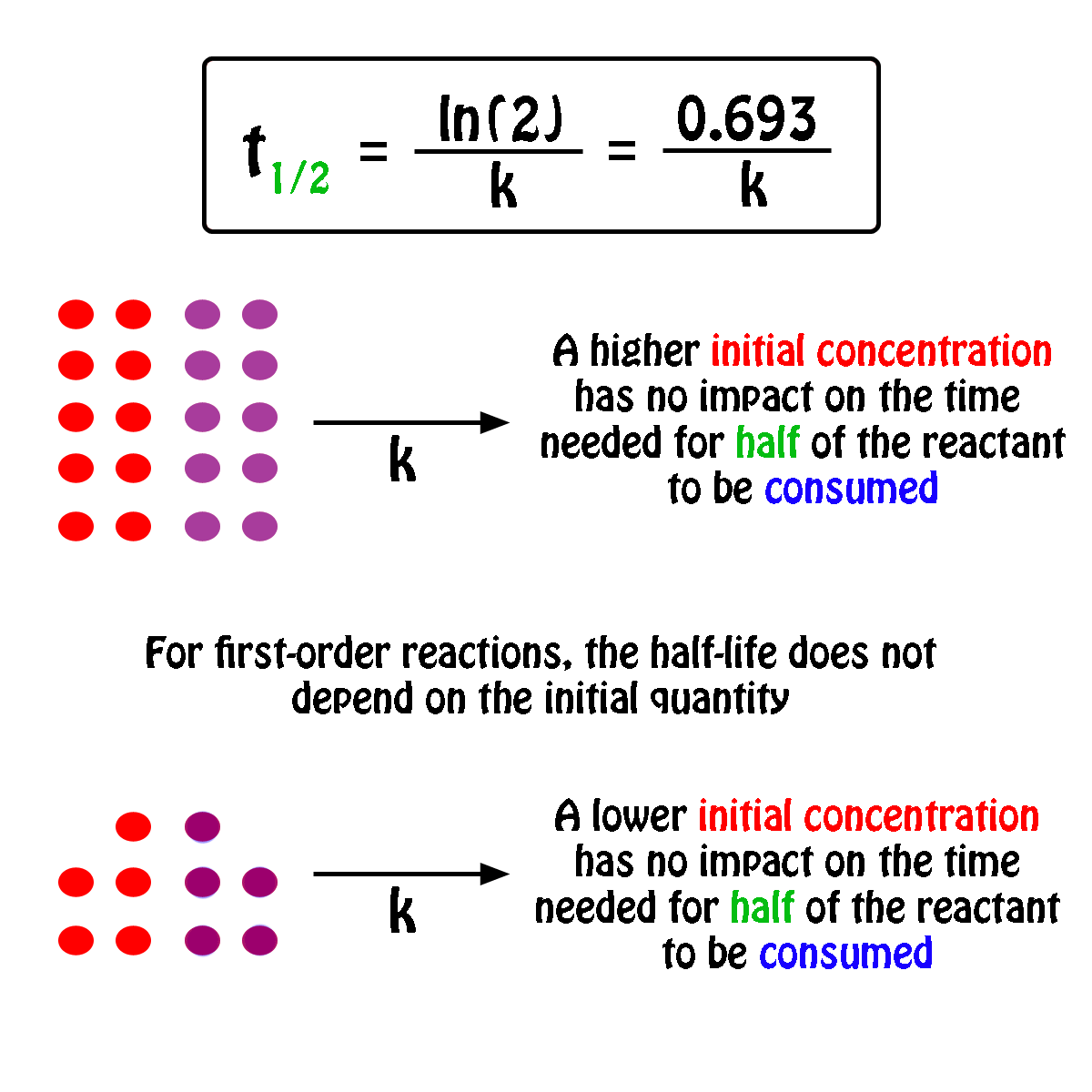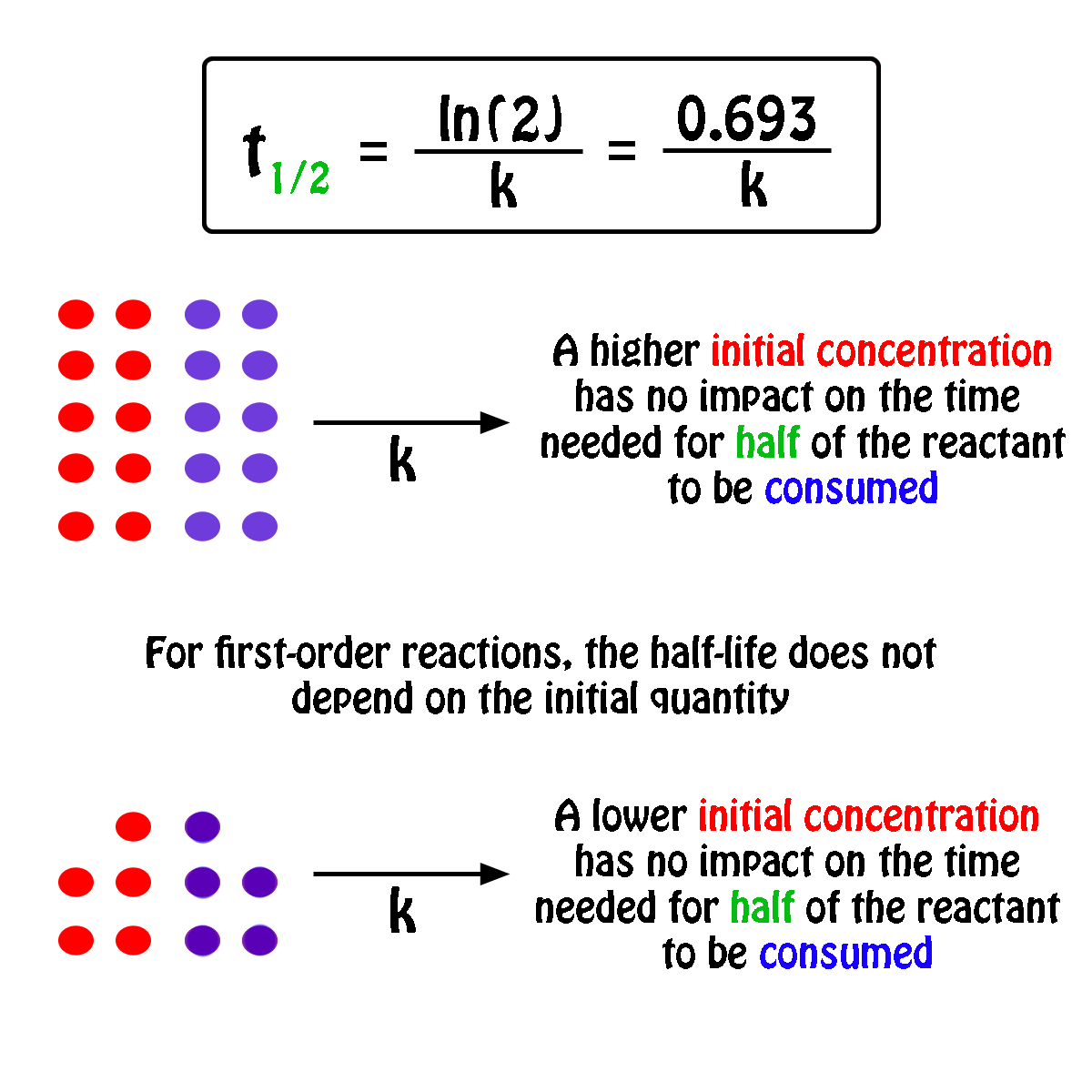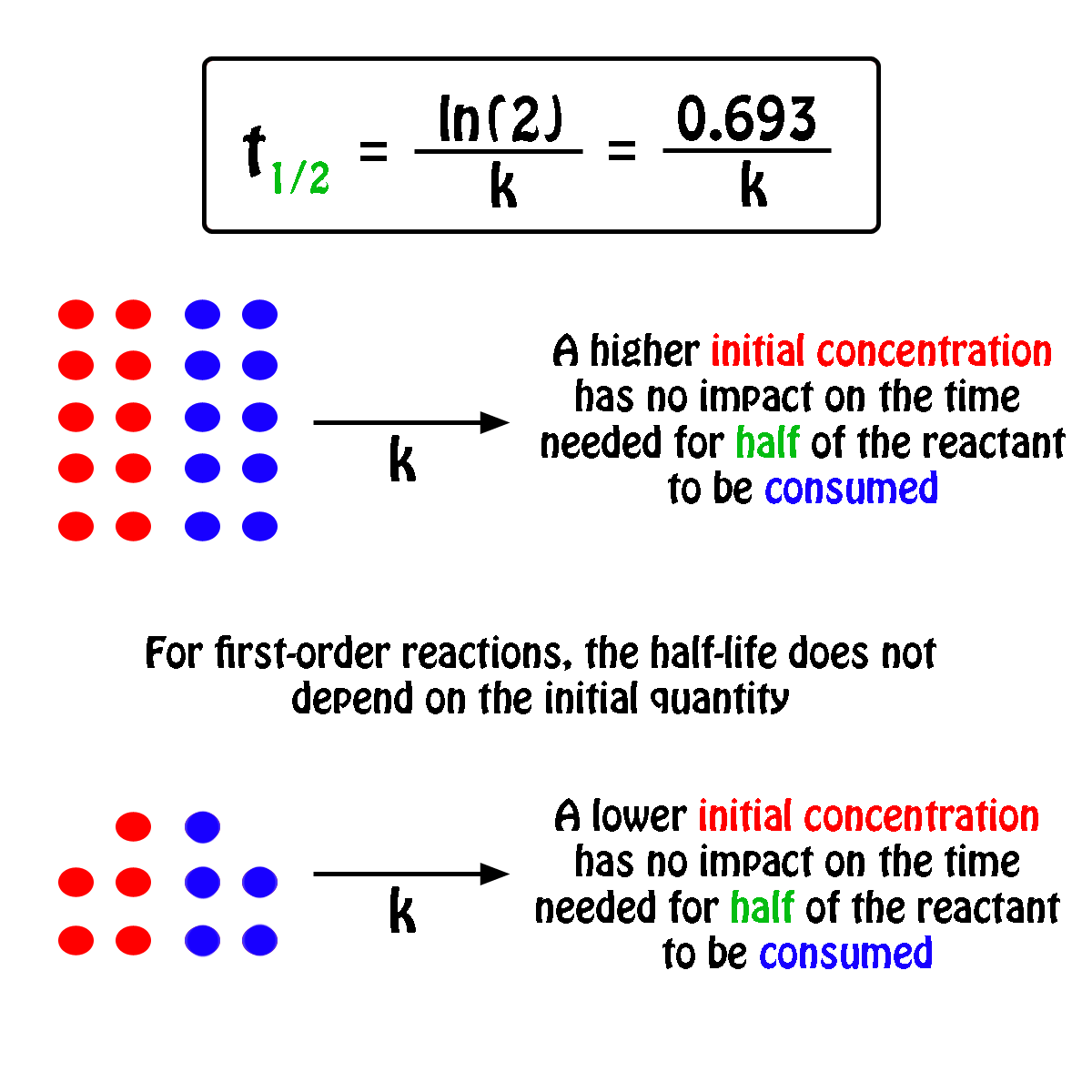
The half-life of a first-order reaction will thus be equal to

`color(green)(|bar(ul(color(white)(a/a)color(black)(t_"1/2" = ln(2)/k)color(white)(a/a)|)))`

An important thing to notice here is that the half-life of a first-order reaction depends exclusively on the rate constant of the reaction.

In other words, the initial concentration of the reactant has no influence on the half-life of the reaction, i.e. the half-life is constant regardless of the concentration of the reactant.