What is sin(inverse tangent(12/5)?
2 Answers
Explanation:
(with the hypotenuse caculated using the Pythagorean Theorem).
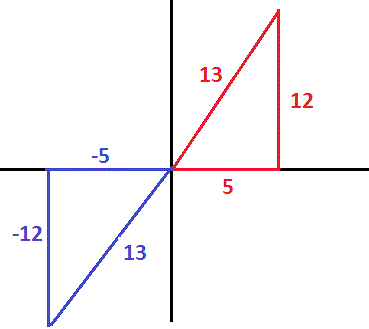
Since
Explanation:
From the trig identity
Since
Taking the least common multiple,
Inverting both sides
Subsituting
Taking the root
To pick the sign we look at the range of the arctangent, it only takes arguments on the first and fourth quadrants, during which the cosine is always positive. If, for
Also, protip, you can use either the function with a "^-1" or put an arc before it to notate the inverse trig functions, but usually there's a lot less headache for everybody involved if you use the arc notation. (There's no grounds for mistaking it for other functions).

