Question

What is the area of a triangle base=2 height =4, but its NOT a right triangle?

Answer 1

Area of a triangle is `1/2 xx base xx height`
(there is no requirement that the triangle be a right triangle for this formula)
The given triangle has an area of 4

Explanation:

Only continue if you don't understand why
`color(white)("XXXX")` `"Area"_"triangle" = 1/2xx"base"xx"height"`

Consider the two triangles below:

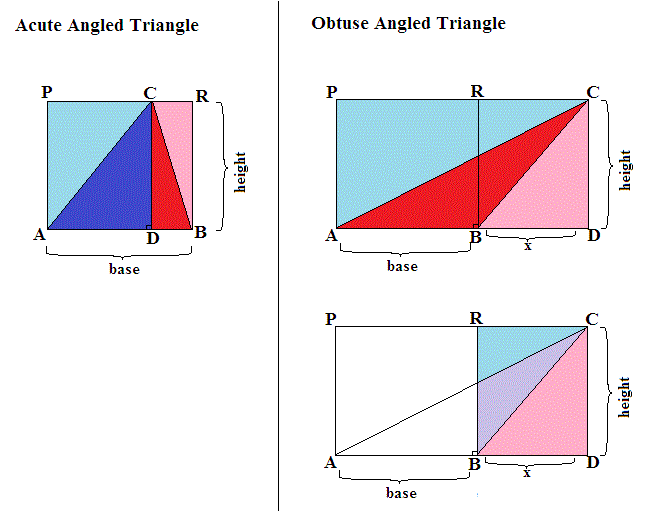
For the Acute Angled Triangle ABC
`triangle ABC` is composed of `triangle ADC` and `triangle DBC`

`triangle ADC = 1/2 square ADCP`
`triangle DBC = 1/2 square DBRC`

`triangle ABC`
`color(white)("XXXX")` `= 1/2 (square ADCP + square DBRC)`

`color(white)("XXXX")` `= 1/2 (square ABRP)`

and since the Area of `square ABRP = "base"xx"height"`

`color(white)("XXXX")`Area of `triangle ABC = 1/2 xx "base" xx "height"`

For the Obtuse Angled Triangle ABC
following a similar argument:
`triangle ADC = 1/2(square ADCP) = 1/2 ("base" + x) xx "height"`

`triangle BDC = 1/2(square BDCR) = 1/2 x xx "height"`

`triangle ABC = triangle ADC - triangle BDC`

Area of `triangle ABC`
`color(white)("XXXX")` `= [ 1/2("base"+x)xx "height"] - [1/2[x xx "height"]`

`color(white)("XXXX")` `= 1/2 "base" xx "height"`