What is the area of a triangle with sides 10, 10 and 16?

1 Answer
Alan P.
Jun 1, 2015

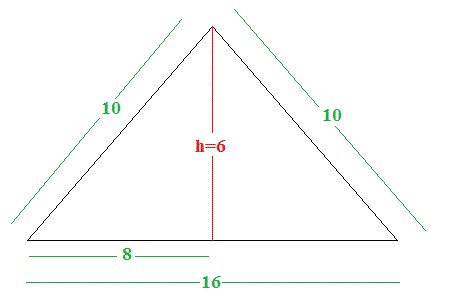
The height of a triangle with sides 10, 10, and 16, if we use 16 as the base is 6 (Pythagorean Theorem and diagram below).

Therefore the area of the triangle is
#A=1/2bh = 1/2*16*6 = 48#
enter image source here

Alternately you could use Heron's formula
#A=sqrt(s(s-a)(s-b)(s-c))# for a triangle with sides #a, b, and c# and a semi-perimeter of #s#.

In this case #s=18#
and
the area #=sqrt(18(8)(8)(2)) = sqrt(36*8^2) = 6*8 = 48#

Related questions
See all questions in Area of a Triangle
Impact of this question
11869 views around the world
You can reuse this answer
Creative Commons License