What is the area of an equiangular triangle with perimeter 36?
3 Answers
Area=
Explanation:
Perimeter =
Therefore,
Area of an equilateral triangle:
=
=
=
=
Explanation:
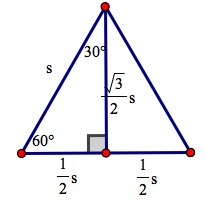
We can see that if we split an equilateral triangle in half, we are left with two congruent right triangles. Thus, one of the legs of one of the right triangles is
If we want to determine the area of the entire triangle, we know that
In your case, the perimeter of the triangle is
Explanation:
In addition to the other answers submitted, you can do this using the trig area rule as well;
In an equilateral triangle, all the angles are
We have the 2 sides and an included angle necessary to use the area rule:



