What is the atomic number of the yet undiscovered element in which the 8s and 8p electron energy levels fill?
1 Answer
If you notice the pattern on the last element on each period, you should see that the number of elements per period goes as the number of quantum numbers allowed for that period (
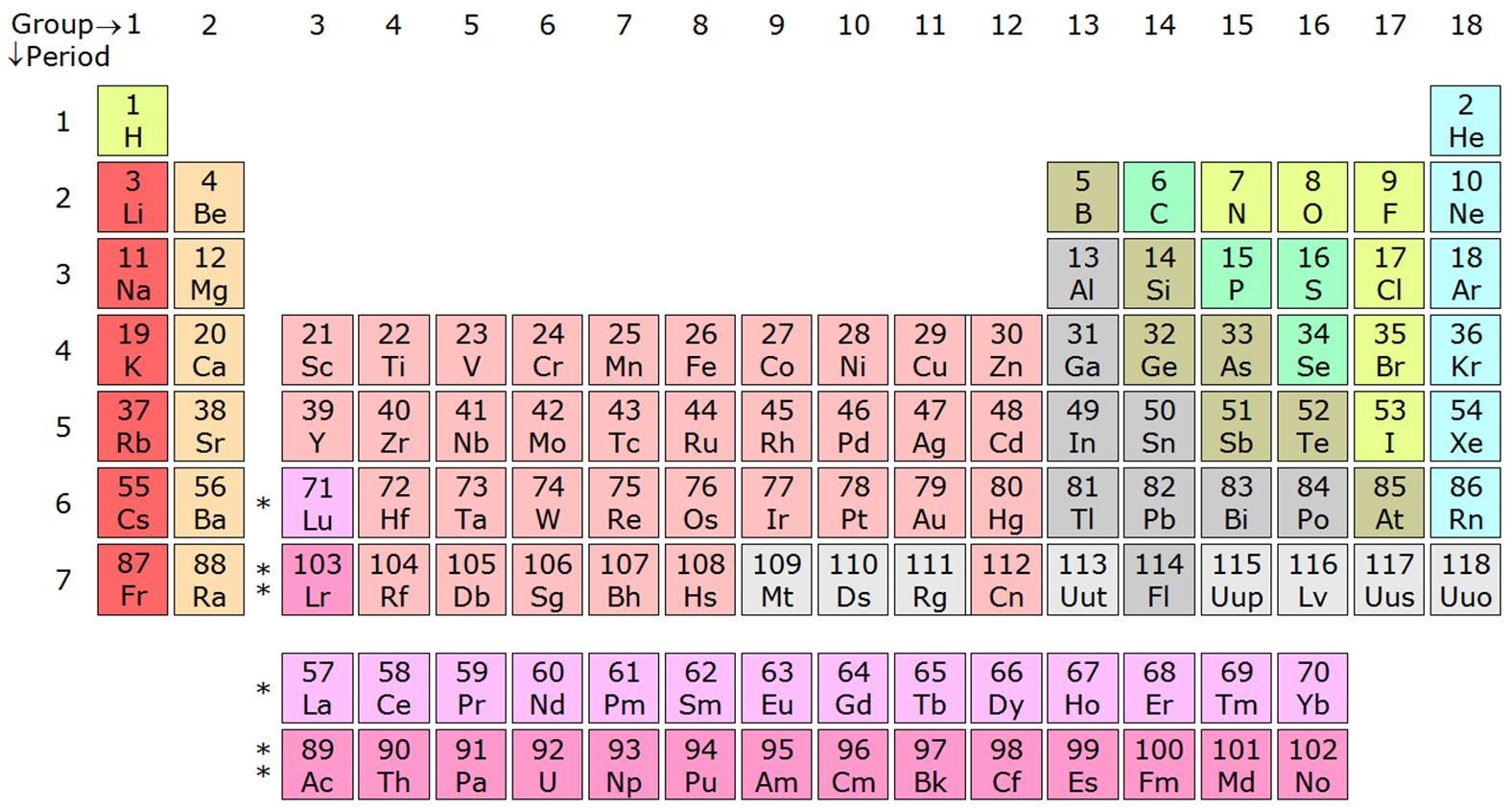
In other words:
#0 + color(green)(2) = 2# #2 + color(green)(8) = 10# #10 + color(green)(8) = 18# #18 + color(green)(18) = 36# #36 + color(green)(18) = 54# #54 + color(green)(32) = 86# #86 + color(green)(32) = 118# #118 + color(green)(?) = "answer"#
So we need to determine the total number of quantum numbers
Refer to this answer for a review of the quantum numbers.
- If
#n = 8# , then#l# takes on values in the set#{0, 1, . . . , n-1} = {0, 1, . . . , 7}# . For these values of#l# , we have the corresponding orbital types:#s, p, d, f, g, h, i, j# , for#l = 0,1,2,3,4,5,6,7# , respectively. But we only need up to#g# . - Therefore,
#m_l# takes on values in the set#{0, pm1, . . . , pm7}# . #m_s = pm"1/2"# .
Assuming the
- For the
#8s# ,#m_l = 0# and#m_s = pm"1/2"# . - For the
#8p# ,#m_l = 0, pm1# and#m_s = pm"1/2"# . - For the
#7d# ,#m_l = 0, pm1, pm2# and#m_s = pm"1/2"# . - For the
#6f# ,#m_l = 0, pm1, pm2, pm3# and#m_s = pm"1/2"# . - For the
#5g# ,#m_l = 0, pm1, pm2, pm3, pm4# and#m_s = pm"1/2"# .
So overall, we have
#stackrel(8s)overbrace(1*2) + stackrel(8p)overbrace(3*2) + stackrel(7d)overbrace(5*2) + stackrel(6f)overbrace(7*2) + stackrel(5g)overbrace(9*2)#
#= 2 + 6 + 10 + 14 + 18 = color(green)(50)# .
Therefore, the element right below ununoctium should be

