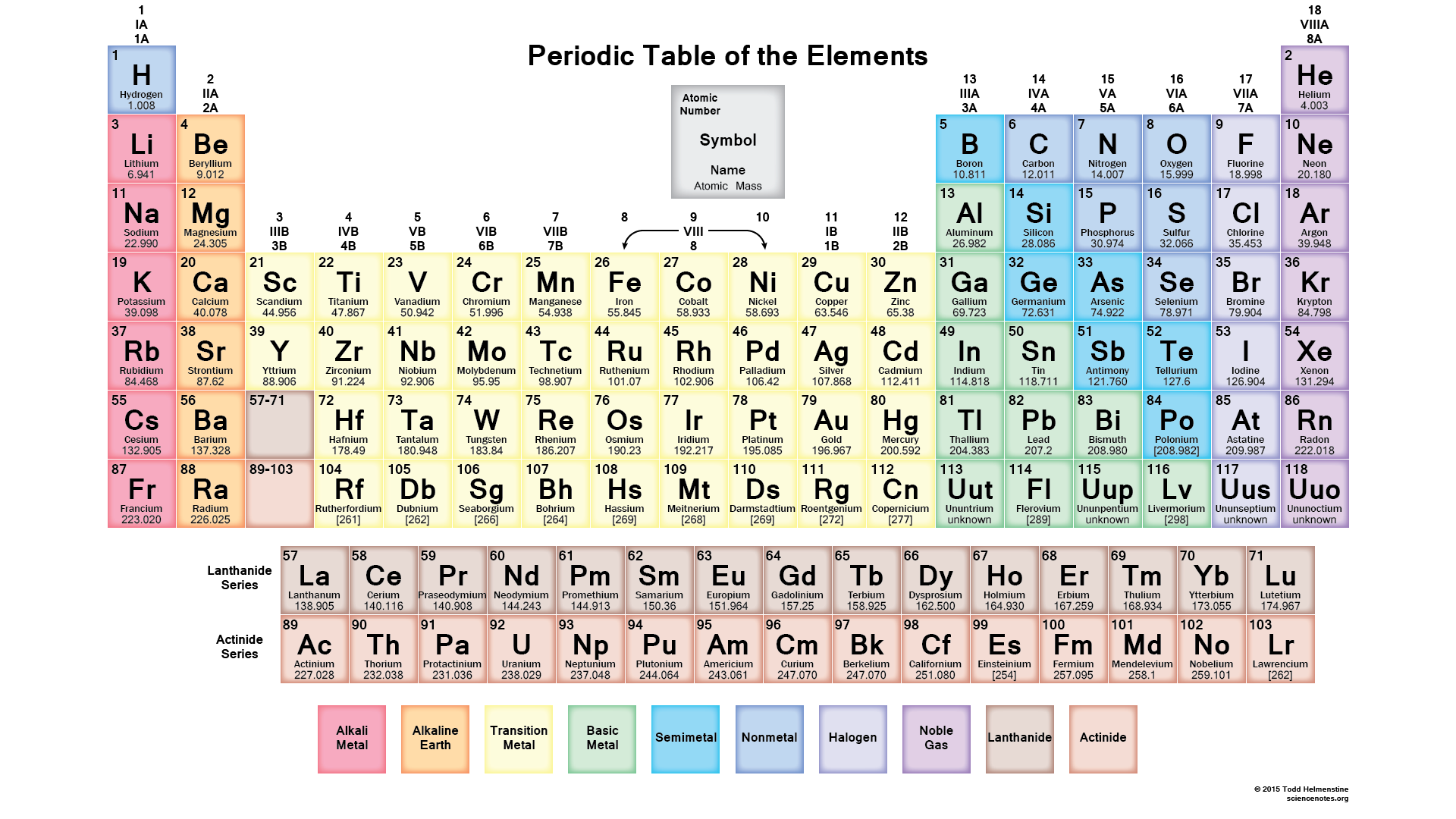
If you recognize where each of the "blocks" of the periodic table are and that each period has a shell number, #n#, you can figure out electron configurations pretty quickly just by looking at the position of the element on the table.
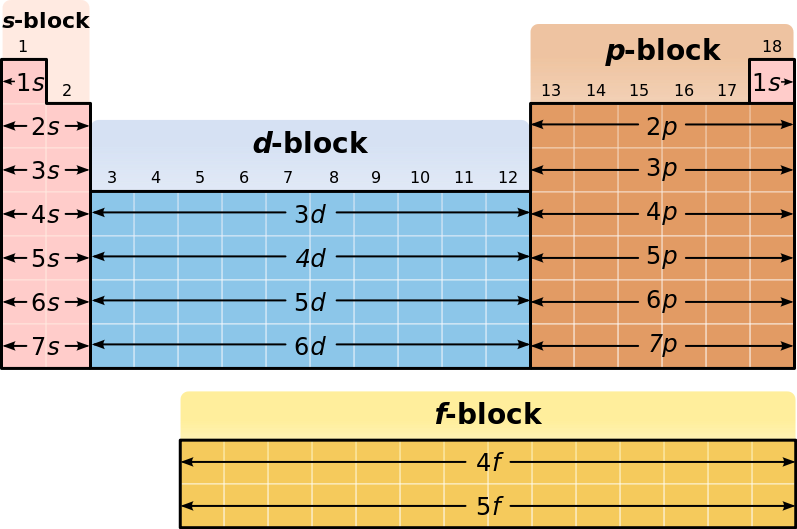
We can see that francium has #87# electrons. Counting down from hydrogen, which is in the #n=1# shell, francium's outermost electrons are "contained" within the #n=7# shell and the element resides in the "#s#-block."
Hydrogen, in the #n=1# shell, has the simple electron configuration of #1s^1#. Helium is #1s^2#. The #n=1# shell contains only the #1s# subshell, containing one #1s# orbital, which can hold a maximum of two electrons. Lithium begins the #n=2# shell. Within the #n=2# shell are the #2s# and #2p# subshells. Sodium begins the #n=3# shell, which contains the #3s, 3p,# and #3d# subshells, each containing their respective orbitals. However, we will see that the #4s# orbital fills with electrons before any of those in the #3d# subshell, as the #4s# orbital is lower in energy than the #3d#s, and it is favorable for electrons to fill low-energy orbitals first (closer to the nucleus).
Francium will fill orbitals all the way up to the #7s# subshell, where it will have a half-filled orbital: #7s^1#.
#1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 3d^(10) 4p^6 5s^2 4d^(10) 5p^6 6s^2 4f^(14 ) 5d^10 6p^6 7s^1#
A short-hand way of writing this is the noble gas configuration, where the noble gas written is to stand for its own electron configuration "plus" whatever is left for the element of concern. For big elements like francium, this is very useful and much more efficient.
#[Rn]7s^1#



