What is the exact value of sec^-1 (sqrt2)?
1 Answer
Jul 14, 2015
Explanation:
If
then
This is a standard trigonometric triangle as pictured below.
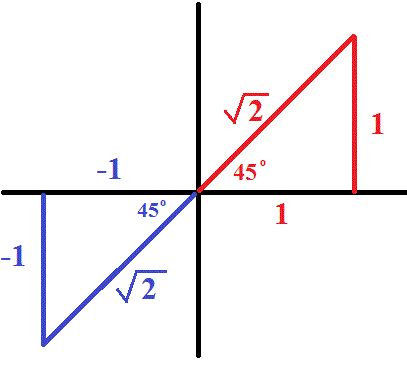
If
then
This is a standard trigonometric triangle as pictured below.
