What is the half-life of a first-order reaction with a rate constant of #7.80xx10^-4 s^(-1)#?
1 Answer
Explanation:
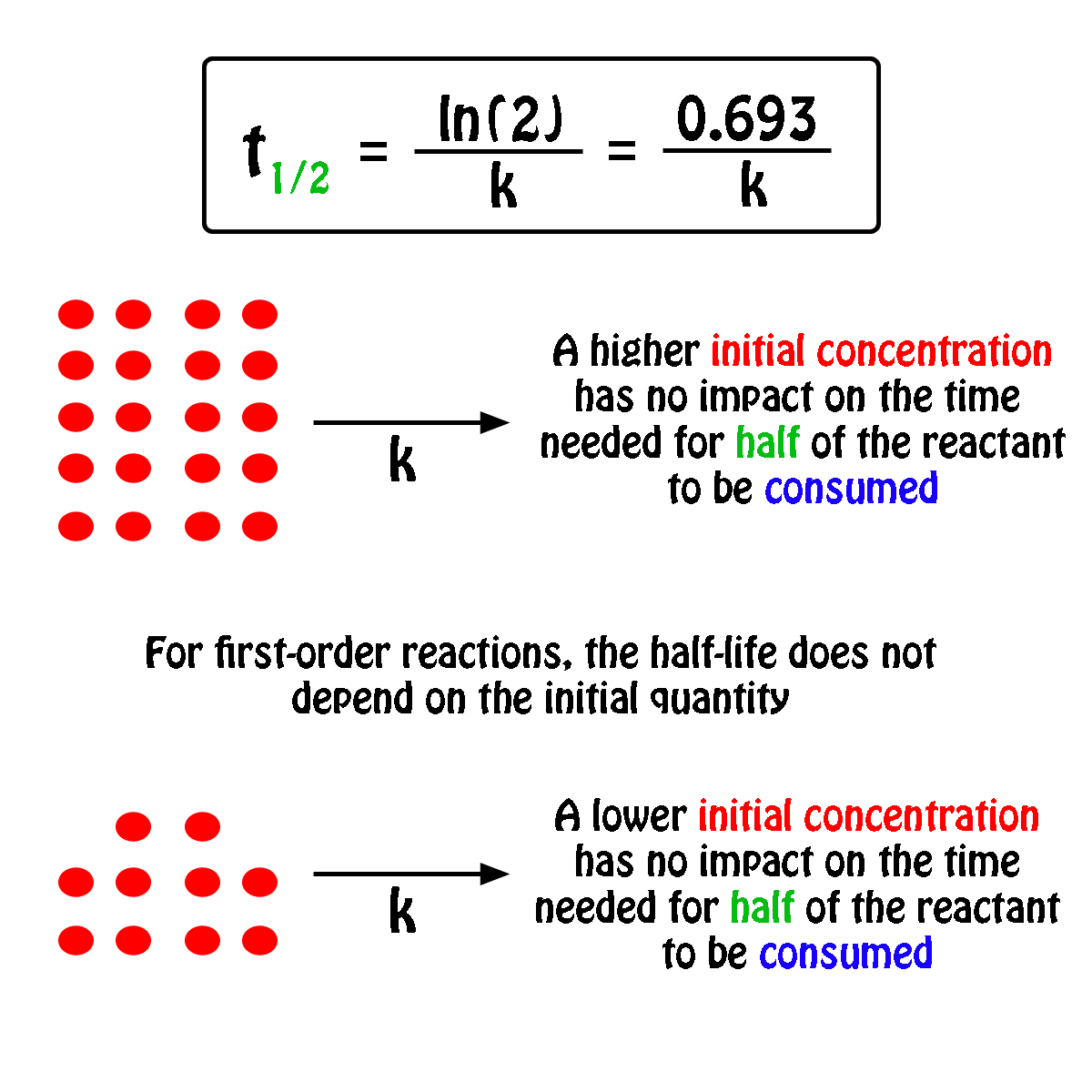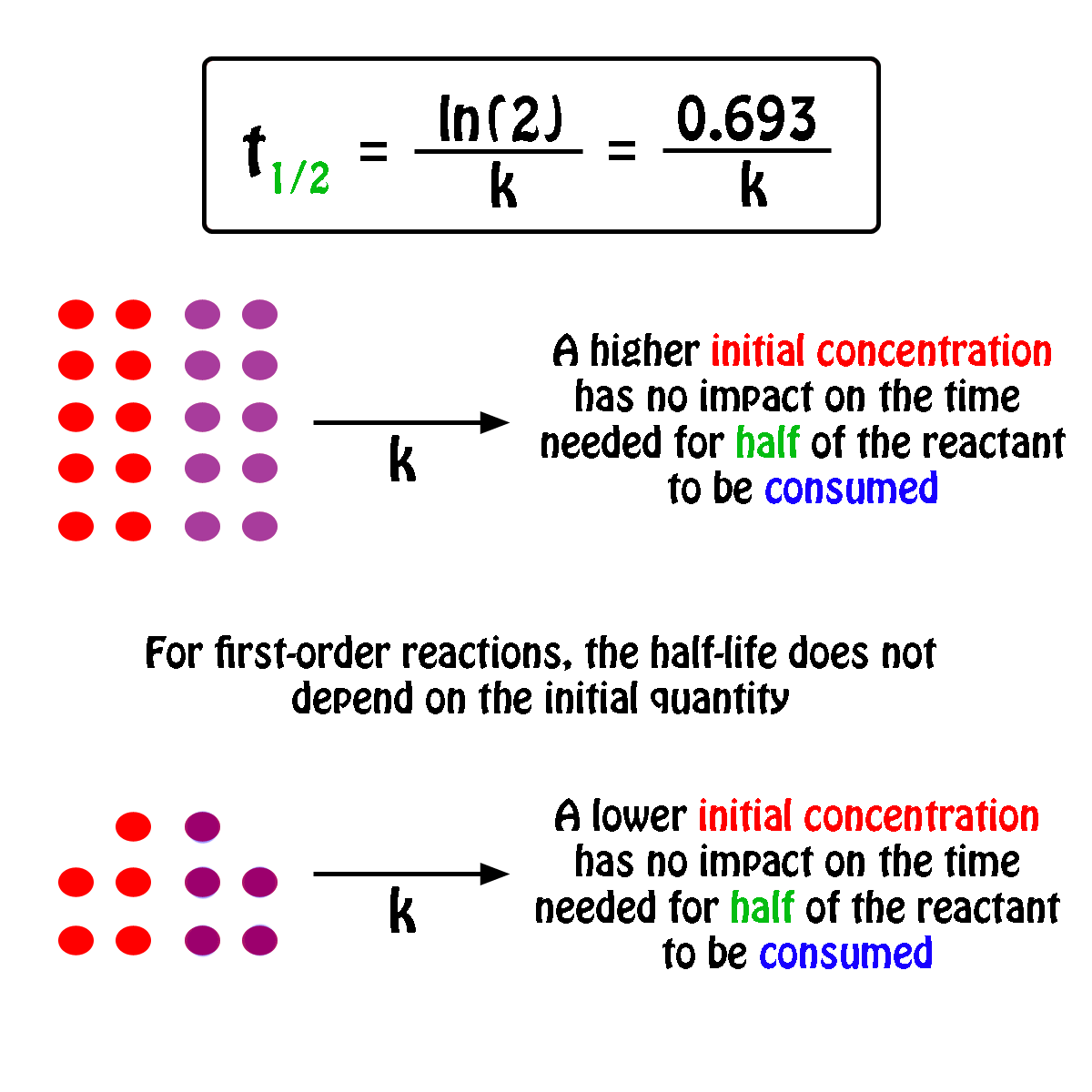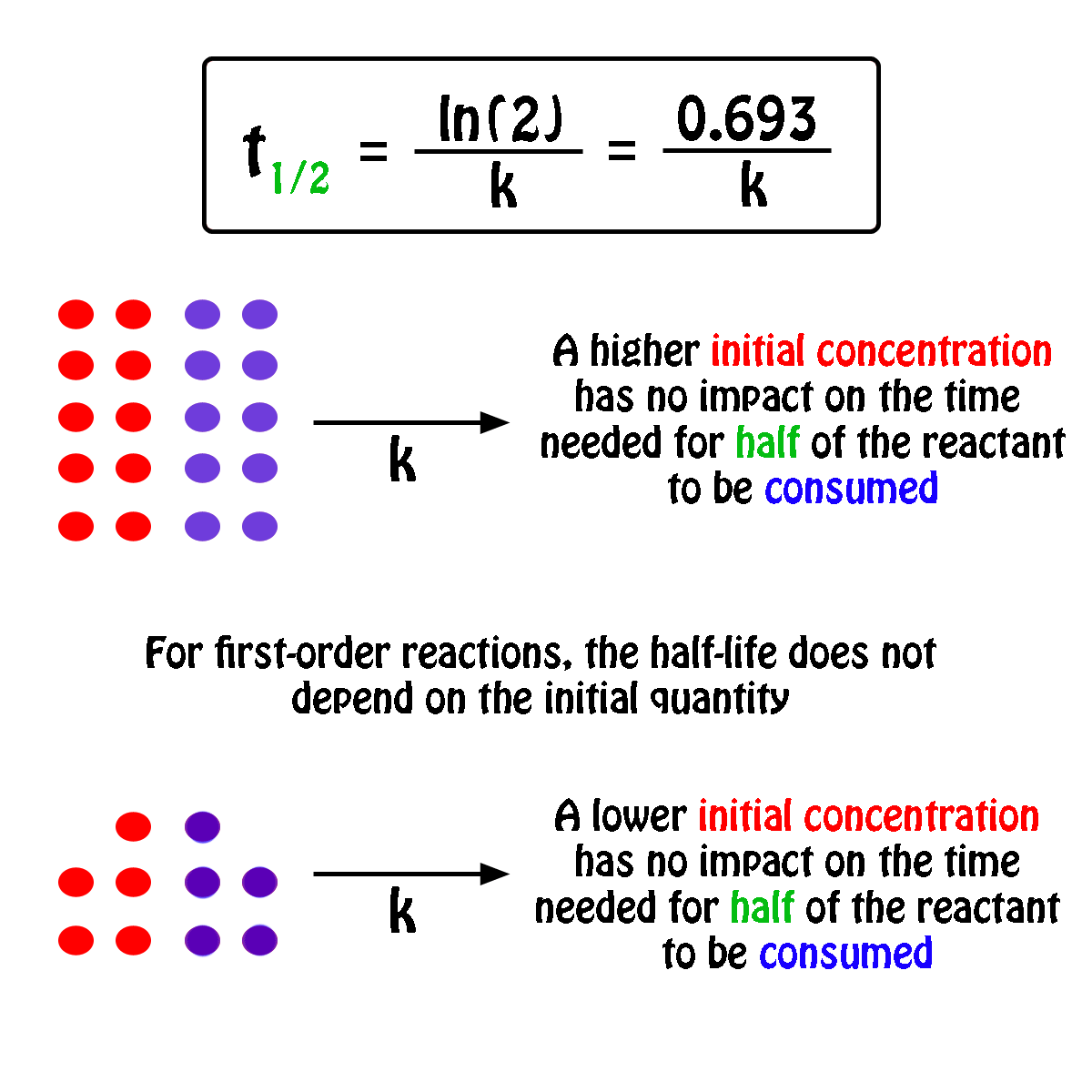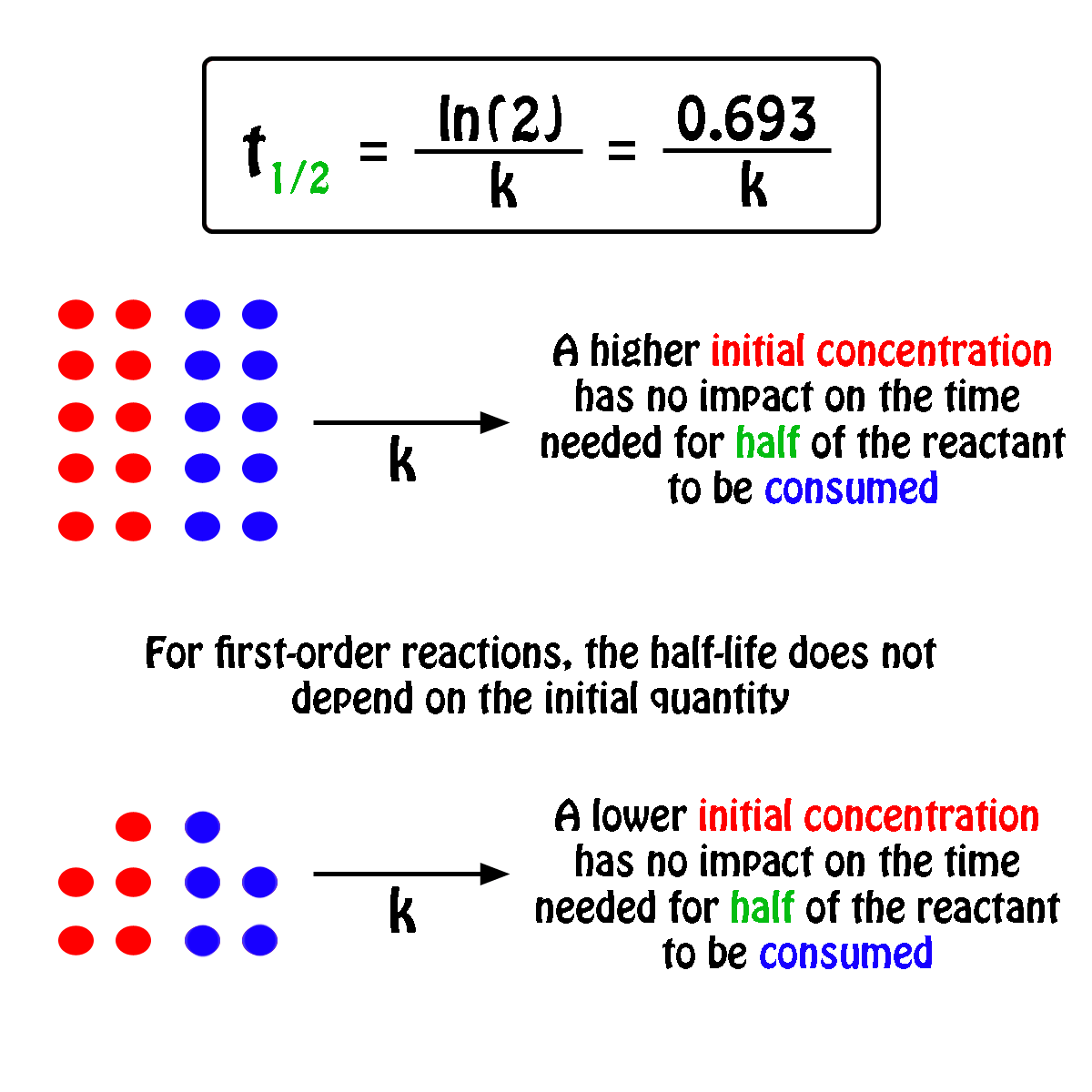
The half-life,
In fact, all you need to know in order to calculate the half-life of a first-order reaction is the rate constant,
#k = 7.80 * 10^(-4)"s"^(-1)#
So, the half-life of a first-order reaction can be calculated by using the equation
#color(blue)(|bar(ul(color(white)(a/a)t_"1/2" = ln(2)/kcolor(white)(a/a)|)))#
Plug in your values to find
#t_"1/2" = ln(2)/(7.80 * 10^(-4)"s"^(-1)) = color(green)(|bar(ul(color(white)(a/a)color(black)("889 s")color(white)(a/a)|)))#
The answer is rounded to three sig figs.
You can thus say that for your reaction, it takes