Question

What is the hybridization for C2H6? my teacher wrote sp-s sigma bond [C-H] and sp-sp sigma bond[C-C]

Answer 1

Either your teacher is incorrect or your molecular formula is incorrect.

IF YOUR FORMULA IS CORRECT

`"C"_2"H"_6` has an `sp^3` hybridization on each carbon because of the four electron groups surrounding each carbon. It made four identical bonds in a perfect tetrahedral geometry, which means it needed four identical orbitals to make those bonds.

Each carbon has to hybridize one `2s` and three `2p` orbitals in order to generate four identical `sp^3` orbitals that are compatible in symmetry with hydrogen's `1s` orbitals.

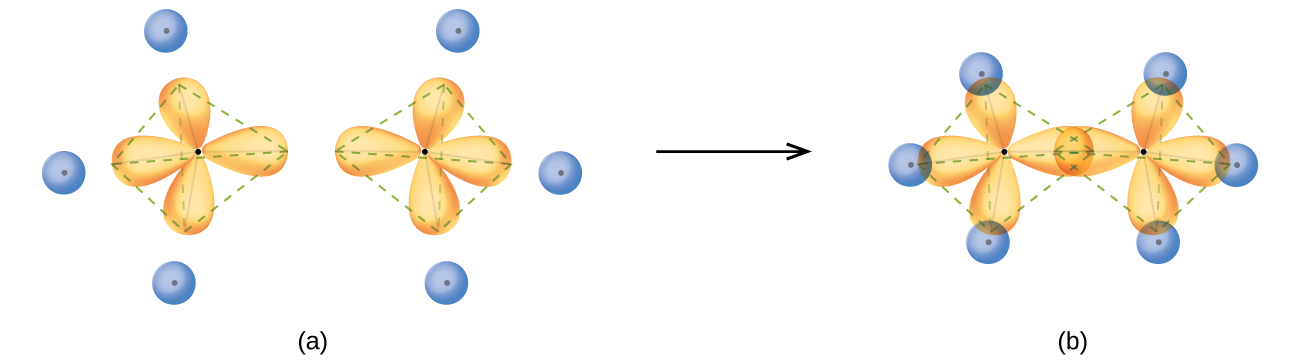
Therefore, each `"C"-"H"` bond in `"C"_2"H"_6` is between an `sp^3` of carbon (YELLOW) and a `1s` of hydrogen (BLUE sphere), i.e. an `sp^3-s` connection (the YELLOW/BLUE overlap in (b)), and each `"C"-"C"` bond is an `sp^3-sp^3` connection (the YELLOW overlap in (b)).

IF YOUR TEACHER WAS CORRECT ON THE HYBRIDIZATIONS

On the other hand, `"C"_2"H"_2` would match your teacher's observations.

With two electron groups on a POLYatomic molecule, each carbon requires only two `sp` lobes and hence only one `sp` hybridized orbital to bond with the other carbon AND a single hydrogen.

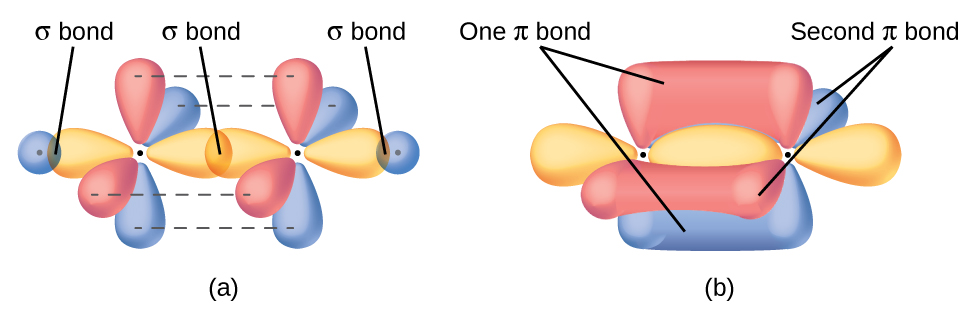
In this case we can see that:

• The `sp` of carbon 1 (YELLOW dumbbell) overlaps with one hydrogen's `1s` (BLUE sphere) to make a `\mathbf(sigma)` bond.
• The `sp` of carbon 1 (YELLOW dumbbell) overlaps with the `sp` of carbon 2 (YELLOW dumbbell) and vice versa to make a `\mathbf(sigma)` bond.
• The `sp` of carbon 2 (YELLOW dumbbell) overlaps with the second hydrogen's `1s` (BLUE sphere) to make a `\mathbf(sigma)` bond.

Each triple bond incorporates an additional `p_x"/"p_x` and `p_y"/"p_y` overlap between carbons 1 and 2, accounting for two `pi` bonds (i.e. `p-p` connections).

Hence, when including those two `p-p` `pi` bonds with the `sp-sp` `sigma` bond between carbons 1 and 2, we have accounted for the the triple bond between carbons 1 and 2.

(One triple bond = 1 `sigma` + 2 `pi` bonds)