What is the Madelung's rule?
1 Answer
Madelung's rule states:
- The energy of an atomic orbital increases with increasing
n + l - For identical values of
n + l , energy increases with increasingn
where
Identical values of
For a
If there are identical
Different
For a
If there are different
This order is based on the total number of nodes in the atomic orbital,
The higher the value of
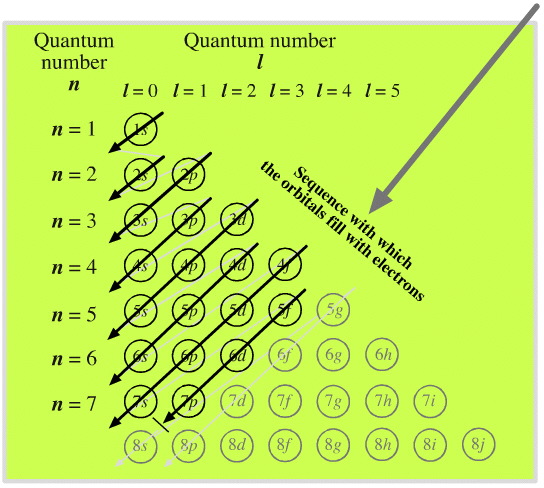
The complete order for filling orbitals according to the Madelung rule is:
The order is summarized in the triangular diagram below.