What is the maximum number of electrons that can occupy the 3d orbitals?
1 Answer
There are five
Explanation:
An orbital is described by the principle quantum number,
The principle quantum number ,
The
#3d# orbital is in the#n=3# shell, just like the#2p# and#2s# orbitals are in the#n = 2# shell.
The angular momentum quantum number ,
Therefore, a
#d# orbital has an#l# value of#2# . It is worth noting that each shell has up to#n-1# types of orbitals.For example, the
#n=3# shell has orbitals of#l=0,1,2# , which means the#n=3# shell contains#s# ,#p# , and#d# subshells. The#n=2# shell has#l=0,1# , so it contains only#s# and#p# subshells.
The magnetic quantum number ,
So, for a
#3d# orbital with#n=3# and#l=2# , we can have#m_1=-2,-1,0,1,2# . This tells us that the#d# orbital has#5# possible orientations in space.If you've learned anything about group theory and symmetry in chemistry, for example, you might vaguely remember having to deal with various orientations of orbitals. For the
#d# orbital, those are#d_(yz)# ,#d_(xy)# ,#d_(xz)# ,#d_(x^2-y^2)# , and#d_(z^2)# . So, we would say that the#3d# subshell contains#5# #3d# orbitals (shown below).
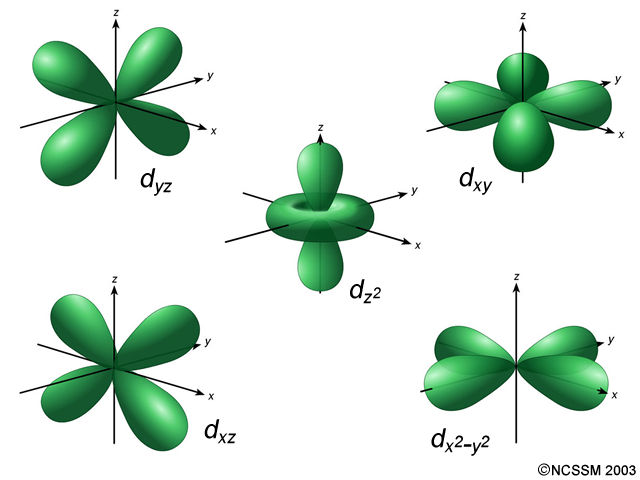
Finally, the electron spin quantum number,
Remember that there are only two electrons to every orbital, and that they should have opposite spins (think Pauli exclusion principle). This tells us that there are two electrons per orbital, or per
#m_l# value, one with an#m_s# value of#+1/2# and one with an#m_s# value of#-1/2# .
(Tl;dr) Thus, as stated above, each individual


