What is the net area between #f(x) = x^2-sqrt(x+1) # and the x-axis over #x in [1, 7 ]#?

Question

1310 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-14T21:53:31

See below.

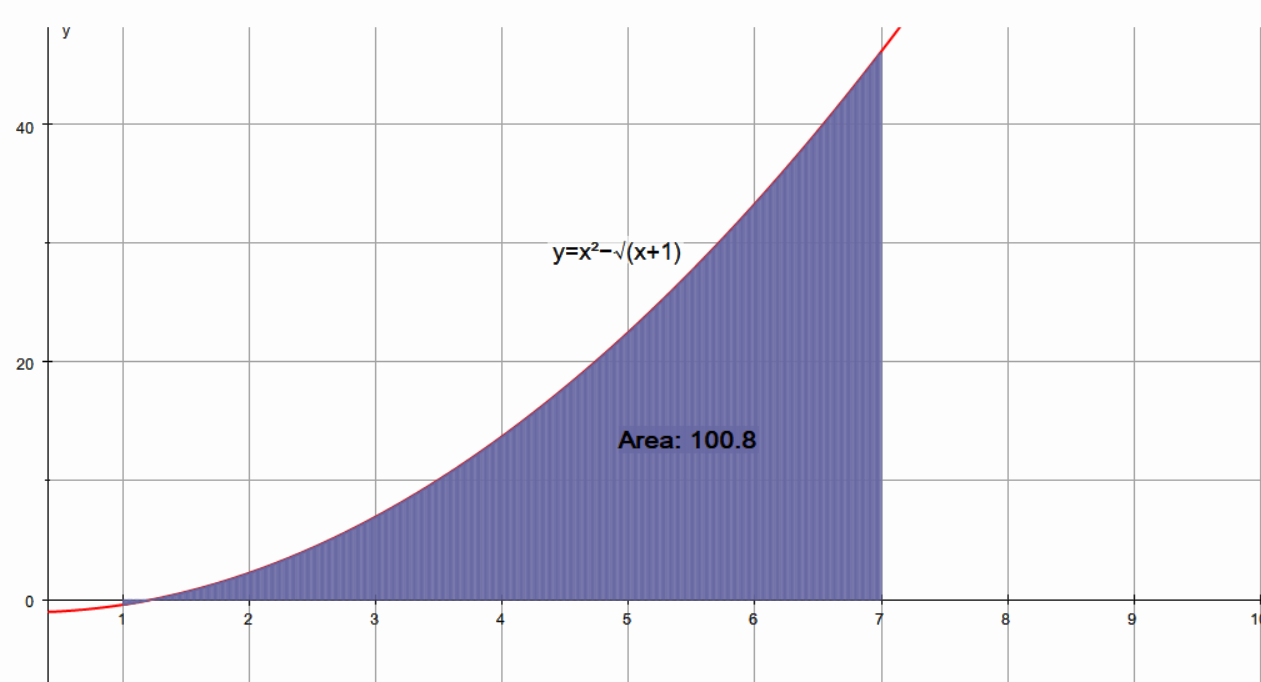
#x-sqrt(x+1)=0#

#x^2-x-1=0=>x=(1+sqrt(5))/2 and x=(1-sqrt(5))/2#

The function is below the x axis in the interval:

#((1-sqrt(5))/2, (1+sqrt(5))/2)#

So we need two integrals:

#A=-int_(1)^((1+sqrt(5))/2)(x^2-sqrt(x+1)) dx+int_((1+sqrt(5))/2)^(7)(x^2-sqrt(x+1)) dx#

#A=-int_(1)^((1+sqrt(5))/2)(x^2-sqrt(x+1)) dx#

#->=[1/3x^3-2/3(x+1)^(3/2)]^((1+sqrt(5)))-[1/3x^3-2/3(x+1)^(3/2)]_(1)#

#=-[1/3((1+sqrt(5))/2)^3-2/3((1+sqrt(5))/2+1)^(3/2)]-[1/3(1)^3-2/3((1+sqrt(5))/2+1)^(3/2)]=0.04738#

#A=int_((1+sqrt(5))/2)^(7)(x^2-sqrt(x+1)) dx#

#->=[1/3x^3-2/3(x+1)^(3/2)]^(7)-[1/3x^3-2/3(x+1)^(3/2)]_((1+sqrt(5))/2)#

#->=[1/3(7)^3-2/3(7+1)^(3/2)]^(7)-[1/3((1+sqrt(5))/2)^3-2/3(((1+sqrt(5))/2)+1)^(3/2)]_((1+sqrt(5))/2)=100.84806#

Area#=100.84806+0.04738=100.89# units squared.

Graph:

enter image source here