Question

What is the order for the reaction `2"N"_2"O"_5(g) -> 4"NO"_2(g) + "O"_2(g)`?

1. What is the order of reaction?
2. What is the concentration of `"O"_2` after `10` minutes?
3. What is `(Delta["NO"_2])/(Deltat)`?
4. What is the half-life of `"N"_2"O"_5`?
5. What is the concentration of `"N"_2"O"_5` after `100` minutes?

Answer 1

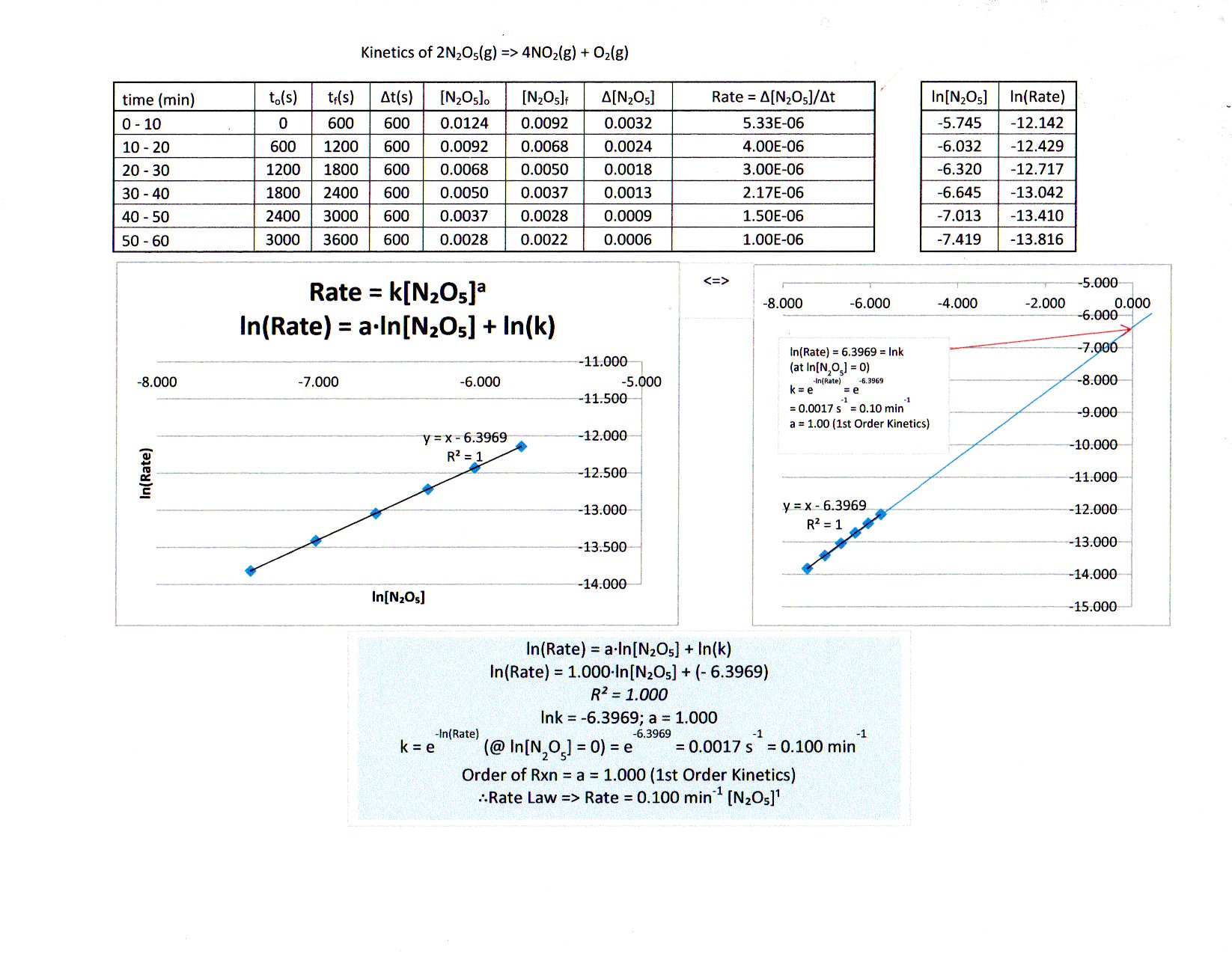
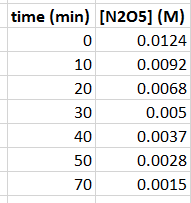
Yes, graphing is the easiest way to do this (or this could be visually challenging!). In fact, learning how to use Excel is a very important skill. I've put a relatively short video on how to use Excel for chemistry here (which goes into graphs near the end):

---

`1)`

If you JUST put time in minutes on the `x` axis and the concentration of `"N"_2"O"_5` in `"M"` on the `y` axis in Excel, it would turn out to be not linear.

But with some trial and error...

• graphing the second order integrated rate law does not work; while it does give a positive slope, the graph is curved (not linear), and thus is of the wrong order.

• graphing the first order integrated rate law works to give a linear graph, confirming it is first order:

I've included the best fit line equation, which is given by:

`bb(underbrace(overbrace(ln["N"_2"O"_5])^(y))_"ln of current conc." = underbrace(overbrace(-k)^(m))_"rate constant"overbrace(t)^(x) + underbrace(overbrace(ln["N"_2"O"_5]_0)^(b))_"ln of initial conc.")`

where `k` is the rate constant, `["N"_2"O"_5]` is the concentration of `"N"_2"O"_5` in `"M"`, and `[" "]_0` means initial concentration. You know that `t` means time in `"min"`.

From looking at the best fit line equation, here is what you can immediately get from it:

`"slope" = -k`

`=> k = -"slope"`

`=> color(blue)(k = "0.0301 min"^(-1))`

`"y-int." = -4.3894`

`=> color(blue)(["N"_2"O"_5]_0) = e^("y-int.") = e^(-4.3894) = color(blue)("0.0124 M")`

And furthermore, the rate law for this would therefore be (from knowing what the order is):

`r(t) = k["N"_2"O"_5]`

`2)` At `t = "10 min"`, to get the concentration of `"O"_2`, we can examine the concentration of `"N"_2"O"_5` remaining, `"0.0092 M"`, and determine the amount of `"O"_2` currently made.

This may or may not be a new concept, but let's consider something called an ICE Table (initial, change, equilibrium), which is normally a way to track the changes in concentration in a reaction on its way to "equilibrium", the point when the reaction has the same rate forwards and backwards.

In the ICE Table below, the coefficients in front of `x` correspond to the coefficients in the chemical reaction.

`2"N"_2"O"_5(g) -> 4"NO"_2(g) + "O"_2(g)`

`"I"" ""0.0124 M"" "" ""0 M"" "" "" ""0 M"`
`"C"" "-2x" "" "" "+4x" "" "" "+x`
`"E"" ""0.0092 M"" "" "4x" "" "" "" "x`

Well, we can track the progress of the reaction using the reaction quotient, `Q`, even though it hasn't reached equilibrium yet. It's the same kind of definition, but we are using the current concentrations instead.

Since we know that the change in concentration of `"N"_2"O"_5` was `2x = "0.0032 M"`, we know that `color(blue)(x = "0.0016 M")` is the change in concentration of `"O"_2`.

And since `"O"_2` started at `"0 M"` (i.e. the reaction started with only reactant), that is its concentration at `bb"10 min"`!

`3)` The initial rate of production of `"NO"_2` comes from the rate law, since we know the rate constant and the starting concentration of `"N"_2"O"_5`:

`r(t) = k["N"_2"O"_5]`

`r(t) = 3.735 xx 10^(-4) "M/min" = |overbrace(-)^"consumption"1/2 overbrace((Delta["N"_2"O"_5])/(Deltat))^"Initial rate"|`

`= overbrace(+)^"production"1/4 overbrace((Delta["NO"_2])/(Deltat))^"Initial rate"`

So, it is:

`color(blue)((Delta["NO"_2])/(Deltat)) = 4/2 xx 3.735 xx 10^(-4) "M/min"`

`= color(blue)(7.47 xx 10^(-4) "M/min")`

`4)` The half-life is known to be at the point where `["N"_2"O"_5] = 1/2["N"_2"O"_5]_0`, i.e. when the reactant concentration has halved. We would obtain this from the integrated rate law:

`ln["N"_2"O"_5] = -kt + ln["N"_2"O"_5]_0`

First, plug in `["N"_2"O"_5] = 1/2["N"_2"O"_5]_0`:

`ln(1/2["N"_2"O"_5]_0) = -kt_"1/2" + ln["N"_2"O"_5]_0`

Now use the property that `lna - lnb = ln(a/b)`:

`ln\frac(1/2cancel(["N"_2"O"_5]_0))(cancel(["N"_2"O"_5]_0)) = -kt_"1/2"`

`=> -ln2 = -kt_"1/2"`

Thus, the first-order half-life is given by:

`=> color(green)(t_"1/2" = (ln2)/k)`

And now, we can get:

`color(blue)(t_"1/2") = (ln2)/("0.0301 min"^(-1))`

`=` `color(blue)("23.03 min")`

`5)` At `"100 min"`, then, we should expect that

`"100 mins passed"/"23.03 min half-life" ~~ 4.34` half-lives passed.

Therefore, the initial concentration `["N"_2"O"_5]_0` should have halved `4.34` times, or been multiplied by `1/2 cdots 1/2 = (1/2)^(4.34) = 1/(2^(4.34))`.

This means the concentration after `"100 min"` is approximately:

`color(blue)(["N"_2"O"_5]_("100 min.")) = "0.0124 M" xx 1/(2^(4.34)) ~~ color(blue)(6.11 xx 10^(-4) "M")`

(or `0.0611 xx 10^(-2) "M"`.)

Answer 2

Kinetic Rate Law for Decomposition of `N_2O_5`
`"Rate" = 0.100 min^-1 [N_2O_5]^1`

Explanation:

Kinetics of `N_2O_5` Decomposition: