We know#" the "color(blue)"Distance Formula" :#
#"The distance between two points"# #P(x_1,y_1) and Q(x_2,y_2)# is:
#color(red)(d(P,Q)=PQ=sqrt((x_1-x_2)^2+(y_1-y_2)^2)...to(1)#
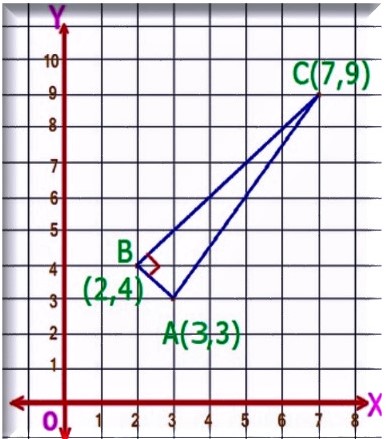
Let , #triangle ABC # ,be the triangle with corners at
#A(3,3) ,B(2,4) and C(7,9) # .
We take, #AB=c, BC=a and CA=b#
So, using #color(red)((1)# we get
#c^2=(3-2)^2+(3-4)^2=1+1=2#
#a^2=(2-7)^2+(4-9)^2=25+25=50#
#b^2=(7-3)^2+(9-3)^2=16+36=52#
It is clear that, #c^2+a^2=2+50=52=b^2#
# i.e. color(red)(b^2=c^2+a^2=>m angle B=pi/2#
Hence, #bar(AC)# is the hypotenuse.
#:.triangle ABC # is the right angled triangle.
#:.#The orthocenter coindes with #B#
Hence, the orthocentre of #triangle ABC# is #B(2,4)#
Please see the graph: