What is the orthocenter of a triangle with corners at #(4 ,3 )#, #(9 ,5 )#, and (7 ,6 )#?

Question

4147 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-02T03:30:14

#color(maroon)("Coordinates of orthocenter " color(green)(O = (19/3, 23/3)#

Find the equations of 2 segments of the triangle
Once you have the equations, you can find the slope of the corresponding perpendicular lines.
You will use the slopes, and the corresponding opposite vertex to find the equations of the 2 lines.
Once you have the equation of the 2 lines, you can solve the corresponding x and y, which is the coordinates of the ortho-centre.

#A (4,3), B(9,5), C(7,6)#

#Slope m_(AB) = (5-3) / (9-4) = 2/5#

#Slope m_(CF) = -1/ m_(AB) = -5/2#

#Slope m_(BC) = (6-5) / (7-9) = -1/2#

#Slope m_(AD) = -1/ m_(BC) = 2#

#"Equation of " vec(CF) " is " y - 6 = -(5/2) * (x - 7)#

#2y - 12 = -5x + 35#

#5x + 2y = 47, " Eqn (1)"#

#"Equation of " vec(AD) " is " y - 3 = 2 * (x - 4)#

#2x - y = 5, " Eqn (2)"#

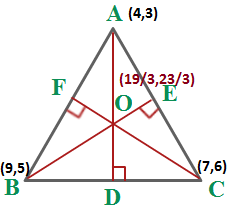
Solving Equations (1) & (2)),

#9x + 2y - 2y = 47 + 10#

#x = 57/9 = 19/3#

#5 * (19/3) + 2y = 47#

#6y = 141 - 95 = 46#

#y = 23/3#

#color(maroon)("Coordinates of orthocenter " color(green)(O = (19/3, 23/3)#

Answer 2 · 2018-05-10T16:24:12

#(19/3, 23/3) #

Let's test the result that the triangle with vertices #(a,b), (c,d)# and #(0,0)# has orthocenter:

#(x,y) = { ac + bd }/{ad - bc} (d-b,a-c)#

Translating #(4,3)# to the origin gives vertices

#(a,b)=(9,5)-(4,3)=(5,2)#

#(c,d)=(7,6)-(4,3)=(3,3)#

#(x,y) = { 5(3) + 2(3) }/{ 5(3) - 2(3)} (1,2) = 21/9(1,2)=(7/3, 14/3)#

We translate back that back

#(7/3, 14/3)+(4,3)= (7/3, 14/3)+ (12/3,9/3)=(19/3, 23/3) #

That matches the other answer -- good.