Question

What is the orthocenter of a triangle with corners at `(4 ,7 )`, `(8 ,2 )`, and (5 ,6 )#?

Answer 1

Orthocenter coordinates `color(red)(O ( 40, 34)`

Explanation:

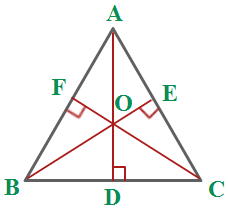
Slope of line segment BC `= m_(BC) = (6-2) / (5-8) = -4/3`

Slope of `m_(AD) = - (1/m_(BC)) = (3/4)`

Equation of altitude passing through A and perpendicular to BC

`y - 7 = (3/4) (x - 4)`

`4y - 3x = 16` Eqn (1)

Slope of line segment AC `m_(AC) = (7-6) / (4-5) = -1`

Slope of altitude BE perpendicular to BC `m_(BE) = -(1/ m_(AC)) = -(1/-1) = 1`

Equation of altitude passing through B and perpendicular to AC

`y - 2 = 1 * (x - 8)`

`y - x = -6` Eqn (2)

Solving Eqns (1), (2) we arrive at the coordinates of orthocenter O

`x = 40, y = 34`

Coordinates of orthocenter `O(40, 34)`

Verification :

Slope of `CF = - (4-8) / (7-2) = (4/5)`

Equation of Altitude CF

`y - 6 = (4/5) (x - 5)`

`5y - 4x = 10` Eqn (3)

Orthocenter coordinates `O ( 40, 34)`

Answer 2

Orthocenter: `(40,34)`

Explanation:

I worked out the semi-general case [here].(https://socratic.org/questions/what-is-the-orthocenter-of-a-triangle-with-corners-at-7-3-4-4-and-2-8)

The conclusion is the orthocenter of the triangle with vertices `(a,b),` `(c,d)` and `(0,0)` is

`(x,y) = { ac + bd }/{ad - bc} (d-b,a-c)`

Let's test it by applying it to this triangle and comparing the result to the other answer.

First we translate (5 ,6) to the origin, giving the two other translated vertices:

`(a,b)=(4,7)-(5,6)=(-1,1)`

`(c,d)=(8,2)-(5,6)=(3,-4)`

We apply the formula in the translated space:

`(x,y) = {-1(3) + 1(-4) }/{-1(-4) - 1 (3) } (-5,-4)= -7(-5,-4)=(35,28)`

Now we translate back for our result:

Orthocenter: `(35,28) + (5,6) = (40,34)`

That matches the other answer!