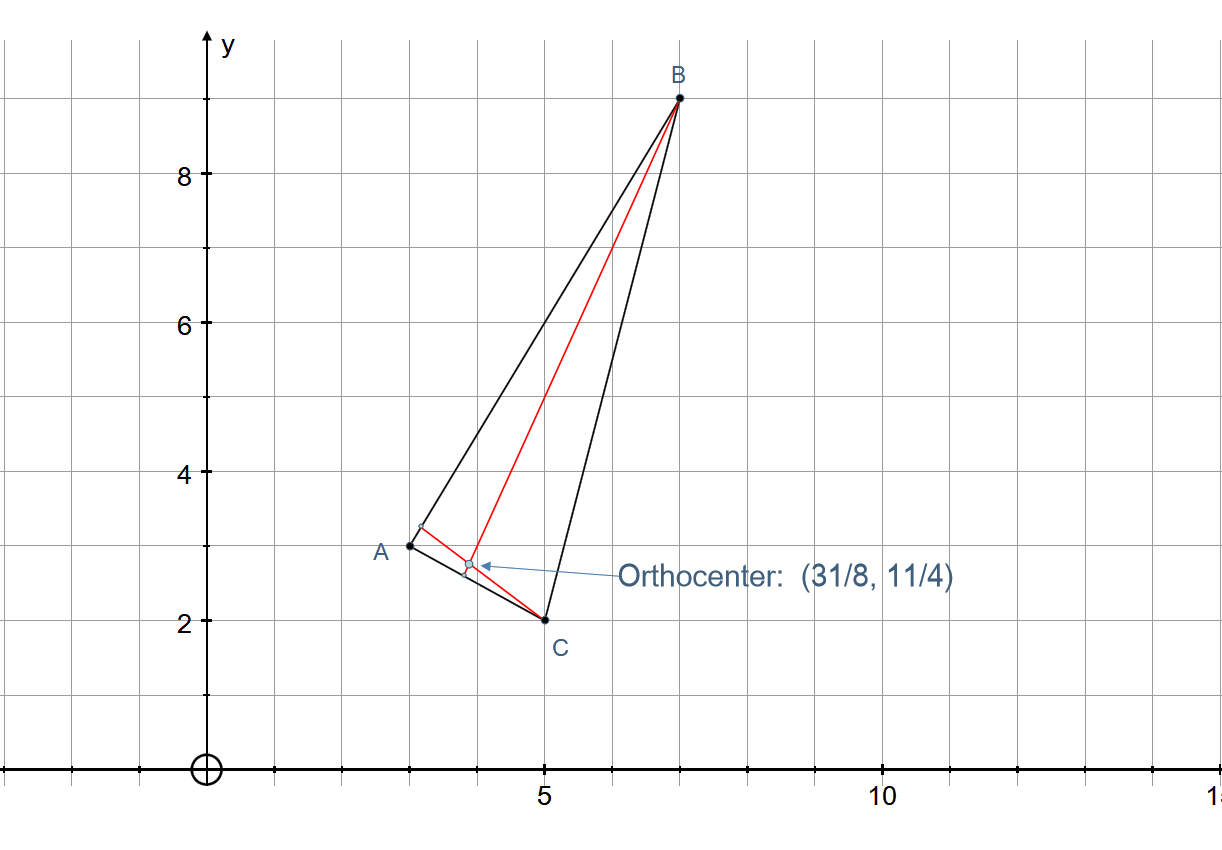
What is the orthocenter of a triangle with corners at #(5 ,2 )#, #(3 ,3 )#, and (7 ,9 )#?

1 Answer
Somebody N.
May 23, 2018

#color(blue)((31/8,11/4)#

Explanation:

The orthocenter is a point where the altitudes of a triangle meet. In order to find this point we must find two of the three lines and their point of intersection. We do not need to find all three lines, since the intersection of two of these will uniquely define a point in a two dimensional space.

Labelling vertices:

#A=(3.3)#

#B=(7,9)#

#C=(5,2)#

We need to find two lines that are perpendicular to two of the sides of the triangle. We first find the slopes of two sides.

#AB# and #AC#

#AB=m_1=(9-3)/(7-3)=3/2#

#AC=m_2=(2-3)/(5-3)=-1/2#

The line perpendicular to AB passes through C. The gradient of this will be the negative reciprocal of the gradient of AB. Using point slope form:

#(y-2)=-2/3(x-5)#

#y=-2/3x+16/3 \ \ \ \[1]#

The line perpendicular to AC passes through B. Gradient negetive reciprocal of AC:

#(y-9)=2(x-7)#

#y=2x-5 \ \ \ \[2]#

We now find the point of intersection of these two lines. Solving simultaneously:

#-2/3x+16/3=2x-5=>x=31/8#

#y=2(31/8)-5=11/4#

So the orthocenter is at:

#(31/8,11/4)#

PLOT:

enter image source here

Related questions
See all questions in Altitudes
Impact of this question
1654 views around the world
You can reuse this answer
Creative Commons License