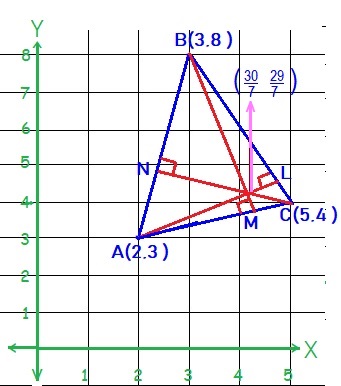
Let #triangle ABC# be the triangle with corners at
#A(2,3), B(3,8) and C(5,4)#.
Let #bar(AL) ,bar(BM) and bar(CN)# be the altitudes of sides
#bar(BC) ,bar(AC) and bar(AB) # respectively.
Let #(x,y) # be the intersection of three altitudes.
Slope of #bar(AB)=(8-3)/(3-2)#=#5=>#slope of #bar(CN)=-1/5[because#altitudes]
#and bar(CN)# passes through #C(5,4)#
So, the equn. of #bar(CN)# is :#y-4=-1/5(x-5)#
#i.e. x+5y=25... to(1)#
Slope of #bar(BC)=(8-4)/(3-5)#=#-2=>#slope of #bar(AL)=1/2[because#altitudes]
#and bar(AL)# passes through #A(2,3)#
So, the equn. of #bar(AL)# is :#y-3=1/2(x-2)#
#i.e. x-2y=-4... to(2)#
Subtracting equn.# :(1)-(2)#
#x+5y=25...to(1)#
#ul(-x+2y=4).to(2)xx(-1)#
#0+7y=29#
#=>color(red)(y=29/7#
From #(2)# we get
#x-2(29/7)=-4=>x=58/7-4=(58-28)/7#
#=>color(red)(x=30/7#
Hence , the orthocenter of triangle is #(30/7, 29/7)#


