Let #triangleABC " be the triangle with corners at"#
#A(8,7), B(2,1) and C(4,5)#
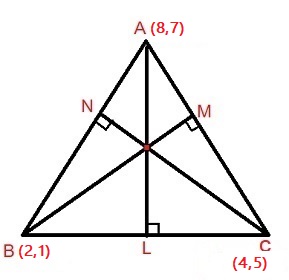
Let #bar(AL) , bar(BM) and bar(CN)# be the altitudes of sides #bar(BC) ,bar(AC) and bar(AB)# respectively.
Let #(x,y)# be the intersection of three altitudes .
Slope of #bar(AB) =(7-1)/(8-2)=1#
#bar(AB)_|_bar(CN)=>#slope of # bar(CN)=-1# ,
# bar(CN)# passes through #C(4,5)#
#:.#The equn. of #bar(CN)# is #:y-5=-1(x-4)#
#i.e. color(red)(x+y=9.....to (1)#
Slope of #bar(BC) =(5-1)/(4-2)=2#
#bar(AL)_|_bar(BC)=>#slope of # bar(AL)=-1/2# , # bar(AL)# passes through #A(8,7)#
#:.#The equn. of #bar(AL)# is #:y-7=-1/2(x-8)=>2y-14=-x+8#
#=>x+2y=22#
#i.e. color(red)(x=22-2y.....to (2)#
Subst. #x=22-2y# into #(1)# ,we get
#22-2y+y=9=>-y=9-22=>color(blue)( y=13#
From equn.#(2)# we get
#x=22-2y=22-2(13)=>x=22-26=>color(blue)(x=-4#
Hence, the orthocenter of triangle is #(-4,13)#

