What is the orthocenter of a triangle with corners at #(9 ,7 )#, #(2 ,9 )#, and (5 ,4 )#?
1 Answer
The orthocenter G is point
Explanation:
The figure below depicts the given triangle and the associated heights (green lines) from each corner.The orthocenter of the triangle is point G.
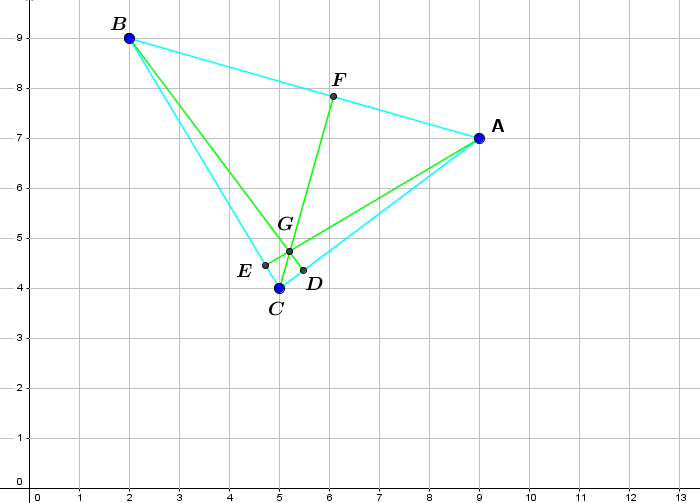
The orthocentre of a triangle is the point where the three altitudes meet.
You need to find the equation of the perpendicular lines that pass through two at least of the triangle vertices.
First determine the equation of each of the sides of the triangle:
From A(9,7) and B(2,9) the equation is
From B(2,9) and C(5,4) the equation is
From C(5,4) and A(9,7) the equation is
Second, you must determine the equations of the perpendicular lines that pass through each vertex:
For AB through C we have that
For AC through B we have that
Now point G is the intersection of the heights hence we have to solve the system of two equations
Hence the solution gives the coordinates of the orthocenter G

