What is the orthocenter of a triangle with corners at #(9 ,7 )#, #(4 ,4 )#, and (8 ,6 )#?

2 Answers
Somebody N.
Dec 13, 2017

See below.

Explanation:

We will call the vertices #A=(4,4)#, #B=(9,7)# and #C=(8,6)#.

We need to find two equations that are perpendicular to two sides and pass through two of the vertices. We can find the slope of two of the sides and consequently the slope of the two of the perpendicular lines.

Slope of AB:

#(7-4)/(9-4)=3/5#

Slope perpendicular to this:

#-5/3#

This has to pass through vertex C, so equation of line is:

#y-6=-5/3(x-8)# , #3y=-5x+58# [ 1 ]

Slope of BC:

#(6-7)/(8-9)=1#

Slope perpendicular to this:

#-1#

This has to pass through vertex A, so equation of line is:

#y-4=-(x-4)# , #y=-x+8# [ 2 ]

Where [1 ] and [ 2 ] intersect is the orthocenter.

Solving [1] and [2] simultaneously:

#3(-x+8)=-5x+58#

#-3x+24=-5x+58#

#-3x+24=5x+58=>x=34/2=17#

Using [2]:

#y=-17+8=-9#

Orthocenter:

#(17 , -9)#

Because the triangle is obtuse the orthocenter is outside of the triangle. this can be seen if you extend the altitude lines until they cross.

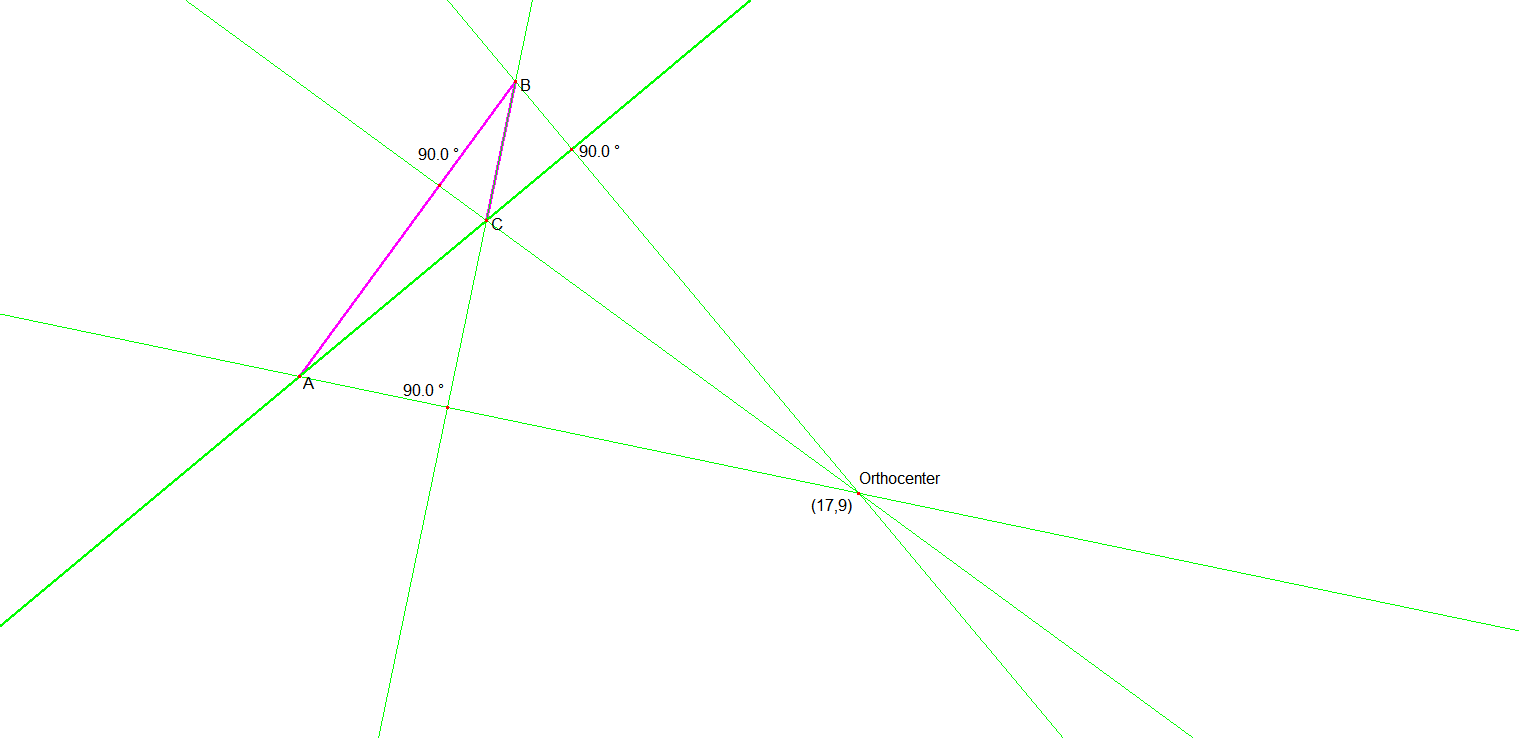
enter image source here

Cesareo R.
Dec 13, 2017

Orthocenter

#x_0 = 17, y_0 = -9#

Circumcenter

#x_0=2,y_0=13#

Explanation:

Orthocenter

Given #p_1, p_2, p_3# and

#vec v_(12), vec v_(13), vec v_(23)# such that

#<< vec v_(12), p_2-p_1 >> = << vec v_(13), p_3-p_1 >>= << vec v_(23), p_3-p_2 >> = 0#

Those vectors are easily obtained, For example

#p_1 = (x_1,y_1)# and #p_2 = (x_2,y_2)# and then

#vec v_(12) = (y_1-y_2, -(x_1-x_2))#

Now we have

#L_1 -> p_1 + lambda_1 vec v_(23)#
#L_2-> p_2 + lambda_2 vec v_(13)#
#L_3->p_3 + lambda_3 vec v_(12)#

Those three lines intersect at the triangle's orthocenter

Choosing #L_1, L_2# we have

#(x_0, y_0) = "arg"(L_1 nn L_2)# or

#p_1+lambda_1 vec v_(23) = p_2 + lambda_2 vec v_(13)#

giving the equations

#{(<< vec v_(13), vec v_(23) >> lambda_1- << vec v_(13), vec v_(13) >> lambda_2 = << p_2-p_1, vec v_(13) >>),(<< vec v_(23), vec v_(23) >> lambda_1- << vec v_(23), vec v_(13) >> lambda_2 = << p_2-p_1, vec v_(23) >>):}#

Now solving for #lambda_1,lambda_2# we have

#lambda_1 = -4, lambda_2 = -13#

and then

#p_0 = p_1 + lambda_1 vec v_(23) = p_2 + lambda_2 vec v_(13) =(17,-9)#

Circumcenter

The circumference equation is given by

#C->x^2+y^2-2x x_0-2y y_0 +x_0^2+y_0^2-r^2=0#

now if #{p_1, p_2,p_3} in C# we have

#{(x_1^2+y_1^2-2x_1 x_0-2y_1 y_0 +x_0^2+y_0^2-r^2=0), (x_2^2+y_2^2-2x_2 x_0-2y_2 y_0 +x_0^2+y_0^2-r^2=0), (x_3^2+y_3^2-2x_3 x_0-2y_3 y_0 +x_0^2+y_0^2-r^2=0):}#

subtracting the first from the second

#x_2^2+y_2^2-(x_1^2+y_1^2)-2x_0(x_2-x_1)-2y_0(y_2-y_1) = 0#

subtracting the first from the third

#x_3^2+y_3^2-(x_1^2+y_1^2)-2x_0(x_3-x_1)-2y_0(y_3-y_1) = 0#

giving the system of equations

#((x_2-x_1, y_2-y_1),(x_3-x_1, y_3-y_1))((x_0),(y_0)) =1/2 ((x_2^2+y_2^2-(x_1^2+y_1^2)),(x_3^2+y_3^2-(x_1^2+y_1^2)))#

Now substituting the given values we get at

#x_0=2,y_0=13#

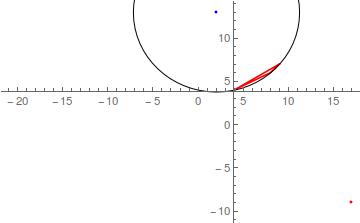
Attached a plot showing the orthocenter (red) and the circumcentercenter (blue).

enter image source here

Related questions
See all questions in Altitudes
Impact of this question
2135 views around the world
You can reuse this answer
Creative Commons License