Question

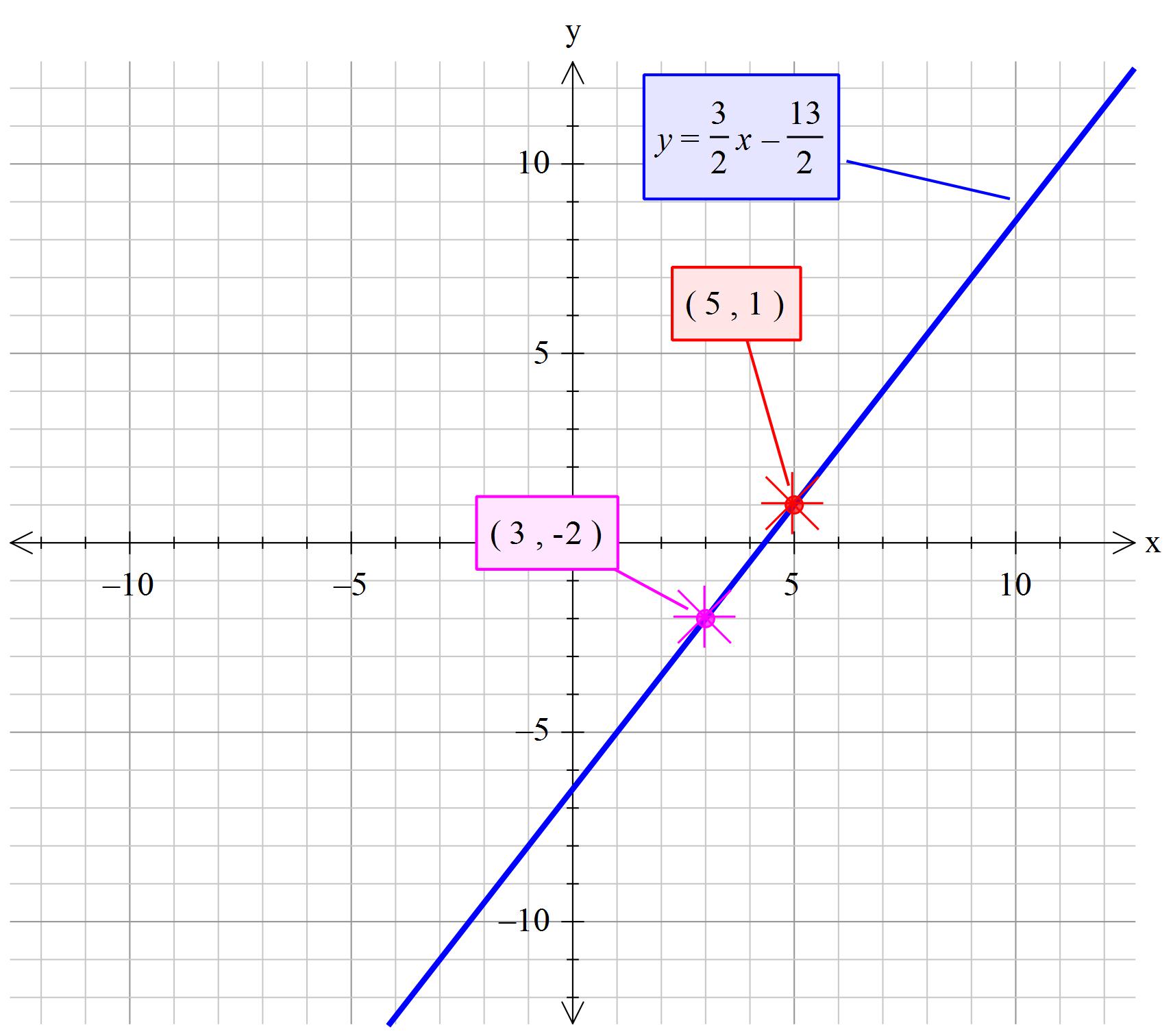
What is the slope-intercept form of the line passing through `(5, 1)` and `(3, -2)`?

Answer 1

`y=3/2x-13/2`

Explanation:

Slope intercept form is:`" "y=mx+c`
where `m` is the gradient and `c` is the y-intercept.

Gradient`->("change in y")/("change in x")`

Let point 1 be `P_1->(x_1,y_1)=(5,1)`
Let point 2 be `P_2->(x_2,y_2)=(3,-2)`

Thus Gradient `->(y_2-y_1)/(x_2-x_1)= (-2-1)/(3-5) =(-3)/(-2)=+3/2`
'.......................................................................................................
So now we have `y=3/2x+c`

To find the value of `c` we substitute in the value of a known point so that there is only 1 unknown.

`color(brown)(=>P_1->y_1=3/2x_1+c)color(blue)( -> 1=3/2(5)+c)`

`" "1=15/2+c`

Subtract `color(magenta)(15/2)` from both sides

`" "color(blue)(1color(magenta)(-15/2)=15/2 color(magenta)(-15/2)+c`

`c=-13/2`
'.........................................................................................................

`" "bar(ul(|color(white)(.)y=3/2x-13/2color(white)(.)|))`