What is the spring constant in parallel connection and series connection?
1 Answer
Parallel.
When two massless springs following Hooke's Law, are connected via a thin, vertical rod as shown in the figure below, these are said to be connected in parallel. Spring 1 and 2 have spring constants
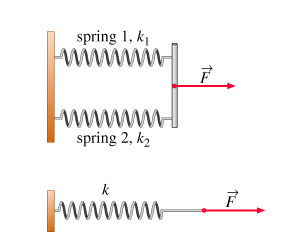
This system of two parallel springs is equivalent to a single Hookean spring, of spring constant
#k=k_1+k_2#
Series.
When same springs are connected as shown in the figure below, these are said to be connected in series. A constant force
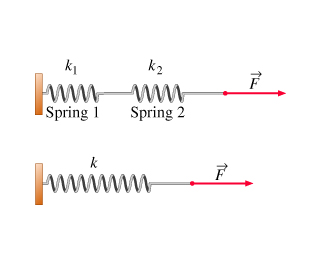
This system of two springs in series is equivalent to a single spring, of spring constant
For spring 1, from Hooke's Law
#F=k_1x_1#
where
Similarly if
#F=k_2x_2#
Total deformation of the system
#x_1+x_2=F/k_1+F/k_2#
#=>x_1+x_2=F(1/k_1+1/k_2)#
Rewriting and comparing with Hooke's law we get
#k=(1/k_1+1/k_2)^-1#

