What is the surface area of a 11 cm high pyramid whose base is an equilateral triangle with a 62 cm perimeter? Show work.
1 Answer
´
Explanation:
To a better understanding refer to the figures below
 I created this figure using MS Excel
I created this figure using MS Excel
 I created this figure using MS Excel
I created this figure using MS Excel
 I created this figure using MS Excel
I created this figure using MS Excel
 I created this figure using MS Excel
I created this figure using MS Excel
We are dealing with a solid of 4 faces, i.e., a tetrahedron.
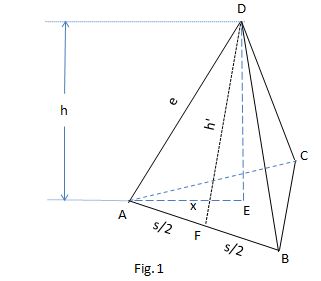
Conventions (see Fig.1)
I called
h the height of the tetrahedron,h"'" the slanted height or height of the slanted faces,s each of the sides of the equilateral triangle of the base of the tetrahedron,e each of the edges of the slanted triangles when nots .
There are also
y , the height of equilateral triangle of the base of the tetrahedron,- and
x , the apothegm of that triangle.
The perimeter of
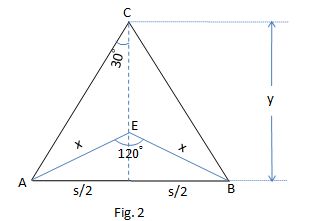
In Fig. 2, we can see that
tan 30^@=(s/2)/y =>y=(s/2)*1/(sqrt(3)/3)=31/cancel(3)*cancel(3)/sqrt(3)=31/sqrt(3)~=17.898
So
S_(triangle_(ABC))=(s*y)/2=(62/3*31/sqrt(3))/2=961/(3sqrt(3))~=184.945
and that
s^2=x^2+x^2-2x*x*cos 120^@
s^2=2x^2-2x^2(-1/2)
3x^2=s^2 =>x=s/sqrt(3)=62/(3sqrt(3)
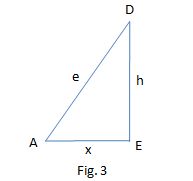
In Fig. 3, we can see that
e^2=x^2+h^2=(62/(3sqrt(3)))^2+11^2=3844/27+121=(3844+3267)/27=7111/27 =>e=sqrt(7111)/(3sqrt(3))
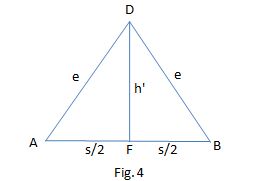
In Fig. 4, we can see that
e^2=h"'"^2+(s/2)^2
h"'"^2=e^2-(s/2)^2=(sqrt(7111)/(3sqrt(3)))^2-(31/3)^2=(7111-3*1089)/27=3844/27
h"'"=62/(3sqrt(3))~=11.932
Area of one slanted triangle
Then the total area is

