Question

What is the the vertex of `y = 3x^2 -x -3`?

Answer 1

The vertex is at `(1/6, -3 1/2)` or about `(0.167, -3.083)`.

Explanation:

`y = 3x^2 - x - 3`

The equation is a quadratic equation in standard form, or `y = color(red)(a)x^2 + color(green)(b)x + color(blue)(c)`.

The vertex is the minimum or maximum point of a parabola . To find the `x` value of the vertex, we use the formula `x_v = -color(green)(b)/(2color(red)(a))`, where `x_v` is the x-value of the vertex.

We know that `color(red)(a = 3)` and `color(green)(b = -1)`, so we can plug them into the formula:
`x_v = (-(-1))/(2(3)) = 1/6`

To find the `y`-value, we just plug in the `x` value back into the equation:
`y = 3(1/6)^2 - (1/6) - 3`

Simplify:
`y = 3(1/36) - 1/6 - 3`

`y = 1/12 - 3 1/6`

`y = 1/12 - 3 2/12`

`y = -3 1/12`

Therefore, the vertex is at `(1/6, -3 1/2)` or about `(0.167, -3.083)`.

Here is a graph of this quadratic equation:

(desmos.com)

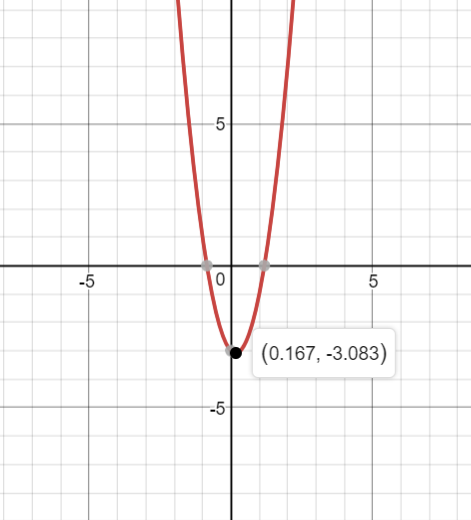
As you can see, the vertex is at `(0.167, -3.083)`.

For another explanation/example of finding the vertex and intercepts of a standard equation, feel free to watch this video:

Hope this helps!