Remember our target form is #y=color(green)m(x-color(red)a)^2+color(blue)b#
with vertex at #(color(red)a,color(blue)b)#
#3y=4x^2+9x-1#
#rarr y=color(green)(4/3)x^2+3x-1/3#
#rarr y=color(green)(4/3)(x^2+9/4x)-1/3#
#rarr y=color(green)(4/3)(x^2+9/4xcolor(magenta)(+(9/8)^2))-1/3color(white)("xx")color(magenta)(-color(green)(4/3)*(9/8)^2)#
#rarr y=color(green)(4/3)(x+9/8)^2-1/3-27/16#
#rarr y=color(green)(4/3)(x-color(red)((-9/8)))^2-16/48-81/48#
#rarr y=color(green)(4/3)(x-color(red)((-9/8)))^2+color(blue)((-97/48))#
which is the vertex form with vertex at #(color(red)(-9/8),color(blue)(-97/48))#
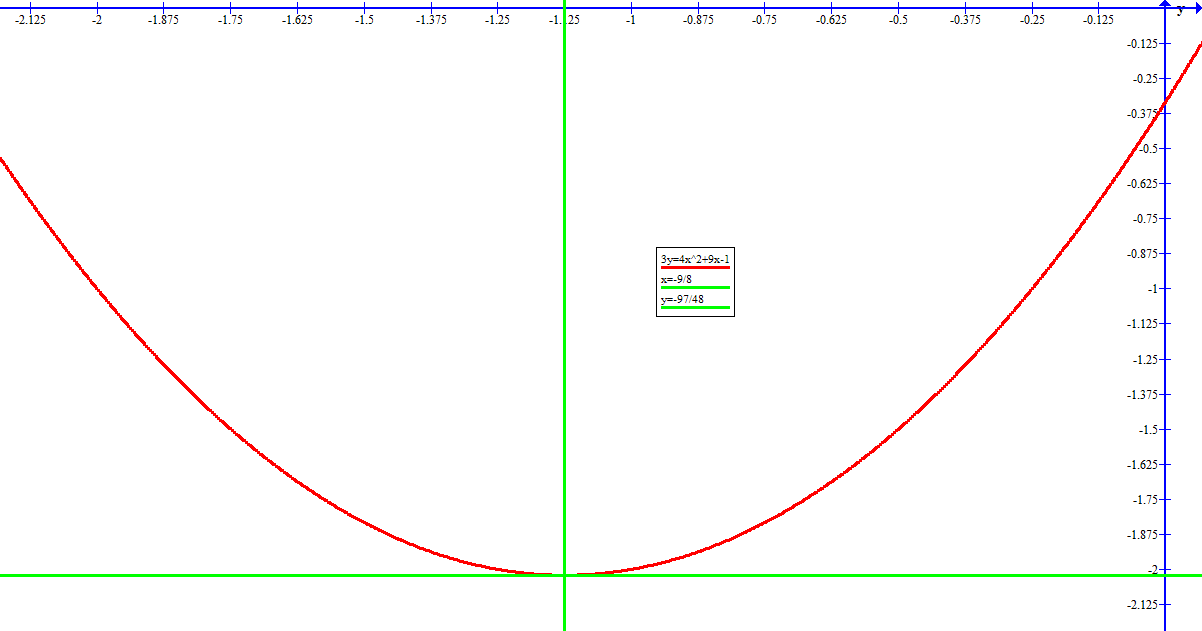
I admit this is not very pretty, so here is a graph of the given equation to demonstrate that this answer is at least reasonable: