What is the vertex form of #4y=5x^2 -7x +3#?
2 Answers
Explanation:
Remember that the vertex form (our target) is in general
Given
We will need to divide everything by
We can now extract the
We want to write
Remember that the squared binomial
since the coefficient of the
our value for
So we need to insert a term of
...but remember that this factor is multiplied by
so to balance thing out we will need to subtract
Our equation now looks like
Writing this with a squared binomial and simplifying the constant terms:
which is our required vertex form with vertex at
For verification purposes here is a graph of the original equation:
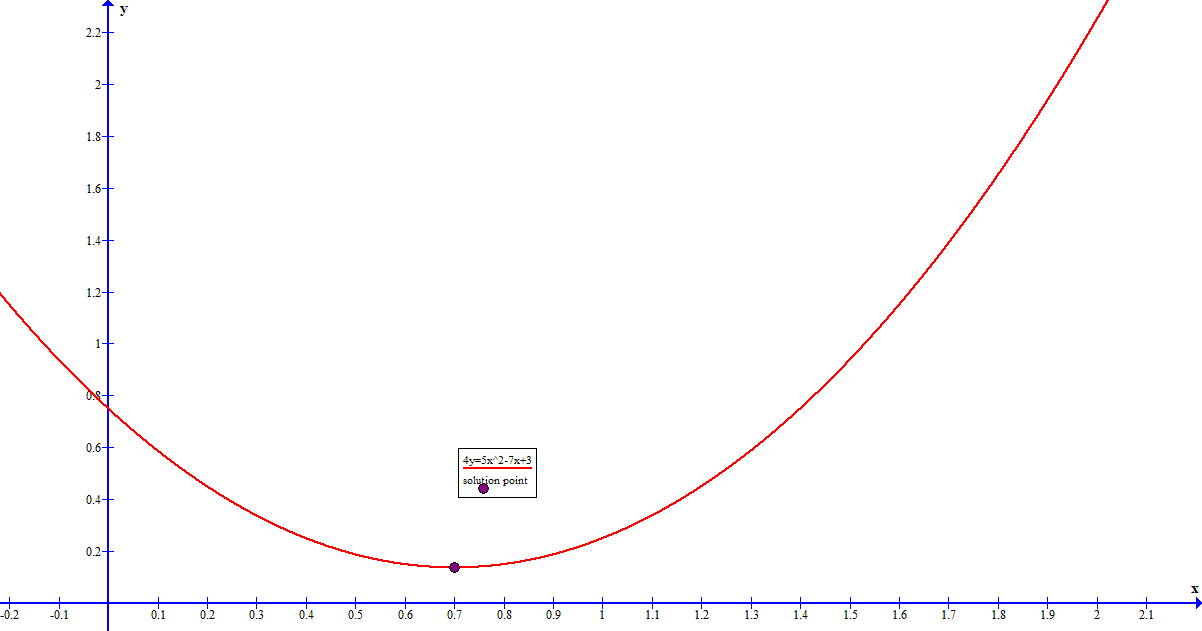
Explanation:
#"the equation of a parabola in "color(blue)"vertex form"# is.
#color(red)(bar(ul(|color(white)(2/2)color(black)(y=a(x-h)^2+k)color(white)(2/2)|)))#
#"where "(h,k)" are the coordinates of the vertex and a"#
#"is a multiplier"#
#"to express "5x^2-7x+3" in this form"#
#"use the method of "color(blue)"completing the square"#
#• "the coefficient of the "x^2" term must be 1"#
#rArr5(x^2-7/5x+3/5)#
#• " add/subtract "(1/2"coefficient of x-term")^2" to"#
#x^2-7/5x#
#5(x^2+2(-7/10)xcolor(red)(+49/100)color(red)(-49/100)+3/5)#
#=5(x-7/10)^2+5(-49/100+3/5)#
#=5(x-7/10)^2+11/20#
#rArr4y=5(x-7/10)^2+11/20#
#rArry=1/4[5(x-7/10)^2+11/20]#
#color(white)(rArry)=5/4(x-7/10)^2+11/80#
