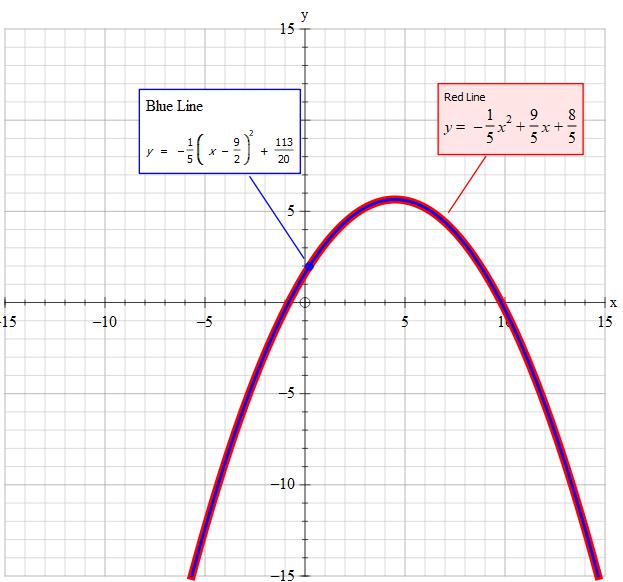
We need the form of: #y="something"# so divide all of both sides by 5 giving:
#y=-1/5x^2+9/5x+8/5" ".......Equation(1)#
Write as:
#color(green)(y=-1/5(x^2-color(red)(9)x)+8/5)#
Halve the #color(red)(9)# and write as:
#color(green)(y=-1/5(x-color(red)(9)/2)^2+k+8/5)" "....Equation(2)#
The #k# is a correction factor as by doing the above you have added a value that is not in the original equation.
Set #color(green)(-1/5(-color(red)(9)/2)^2 +k=0)#
#=> k=+81/20#
Substitute for #k# in #Equation(2)# giving:
#color(green)(y=-1/5(x-color(red)(9)/2)^2+81/20+8/5)" "....Equation(2_a)#
#y=-1/5(x-9/2)^2+113/20#