The general vertex form is
#color(white)("XXX")y=color(green)m(x-color(red)a)^2+color(blue)b#
for a parabola with vertex at #(color(red)a,color(blue)b)#
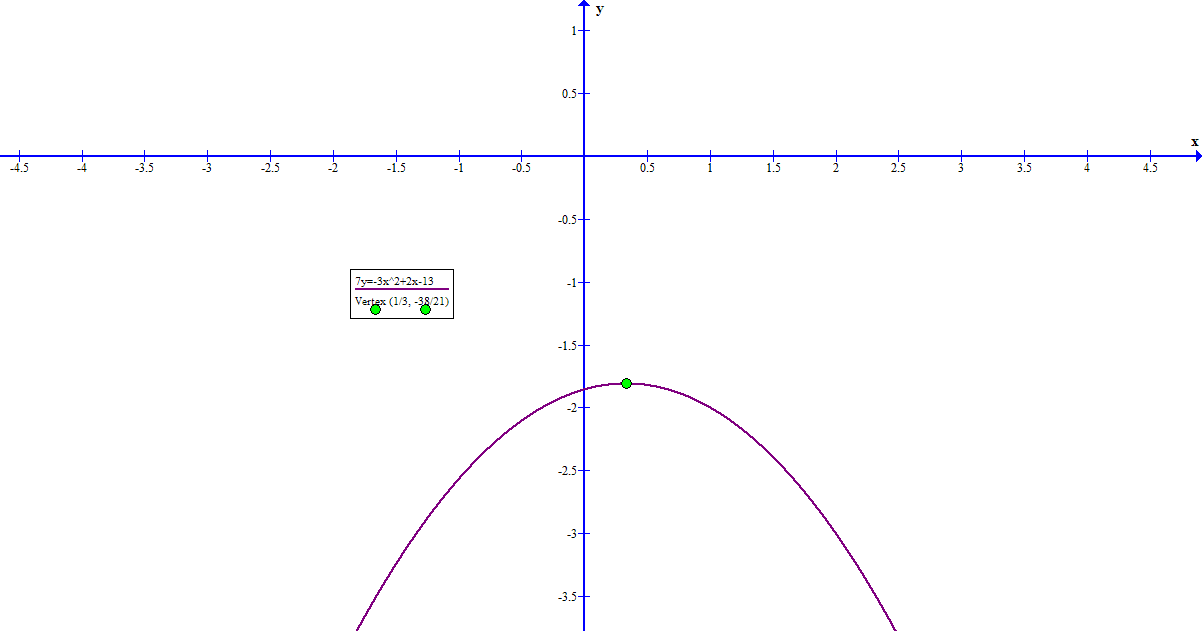
Given #7y=-3x^2+2x-13#
Dividing both sides by #7#
#color(white)("XXX")y=-3/7x^2+2/7x-13/7#
Extracting the "inverse stretch" coefficient, #color(green)m#, from the first 2 terms:
#color(white)("XXX")y=(color(green)(-3/7))(x^2-2/3x)-13/7#
Completing the square
#color(white)("XXX")y=(color(green)(-3/7))(x^2-2/3xcolor(magenta)(+(1/3)^2))-13/7color(magenta)(-(color(green)(-3/7)) * (1/3)^2)#
Simplifying
#color(white)("XXX")y=(color(green)(-3/7))(x-color(red)(1/3))^2+(color(blue)(-38/21))#
which is the vertex form with vertex at #(color(red)(1/3),color(blue)(-38/21))#
For verification purposes here is the graph of the original equation and the calculated vertex point: