What is the vertex form of the equation of the parabola with a focus at (31,24) and a directrix of #y=23 #?
1 Answer
May 28, 2017
#y=1/2(x^2-62x+1008)#
Explanation:
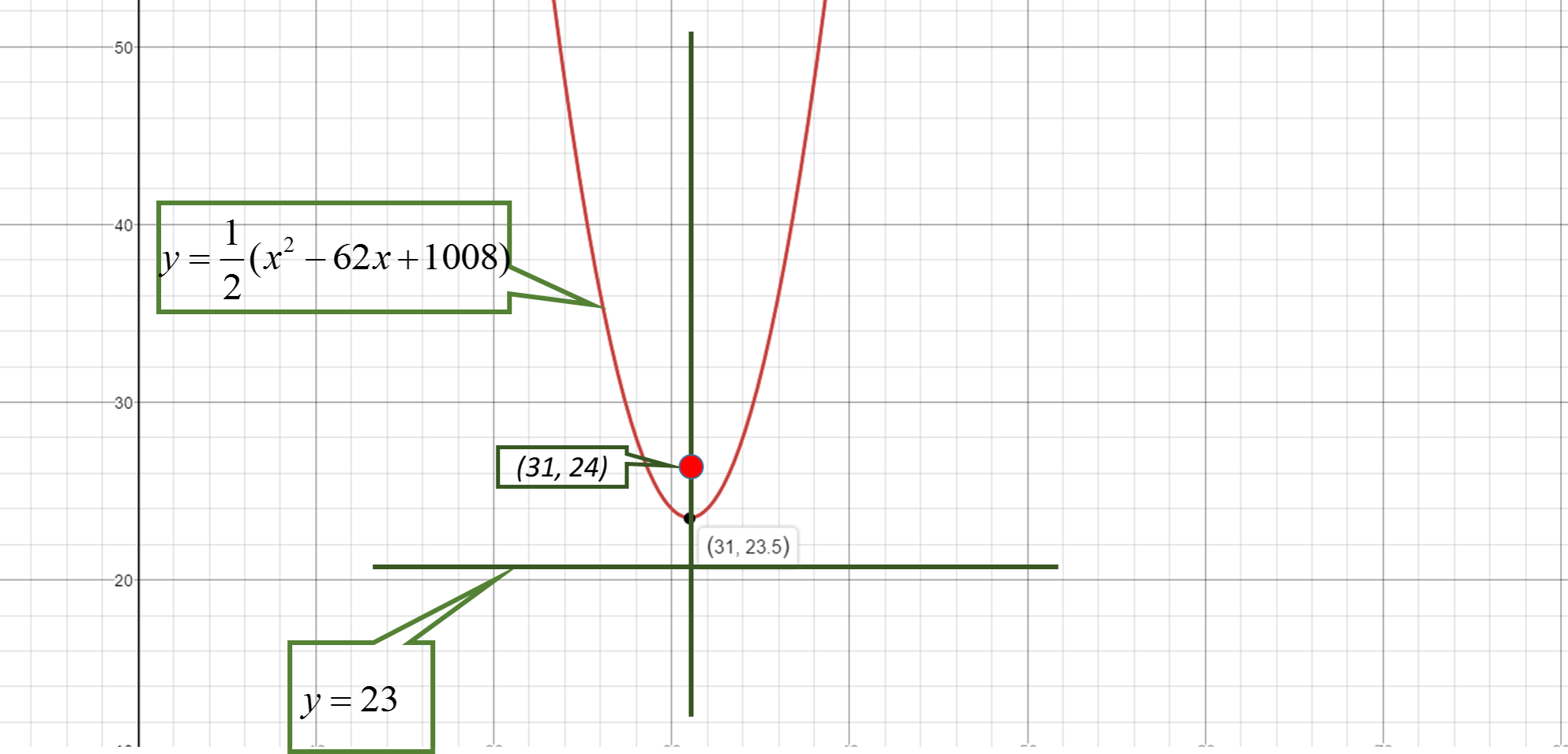
Look at the graph
The parabola is facing upwards, hence
#(x-h)^2=4a(y-k)#
Here
Vertex lies exactly at the middle of focus and directrix.
y coordinate of the vertex
Vertex
#(x-31)^2=4xx0.5xx(y-23.5)#
#x^2-62x+961=2y-47#
#2y-47=x^2-62x+961#
#2y=x^2-62x+961+47#
#y=1/2(x^2-62x+1008)#

