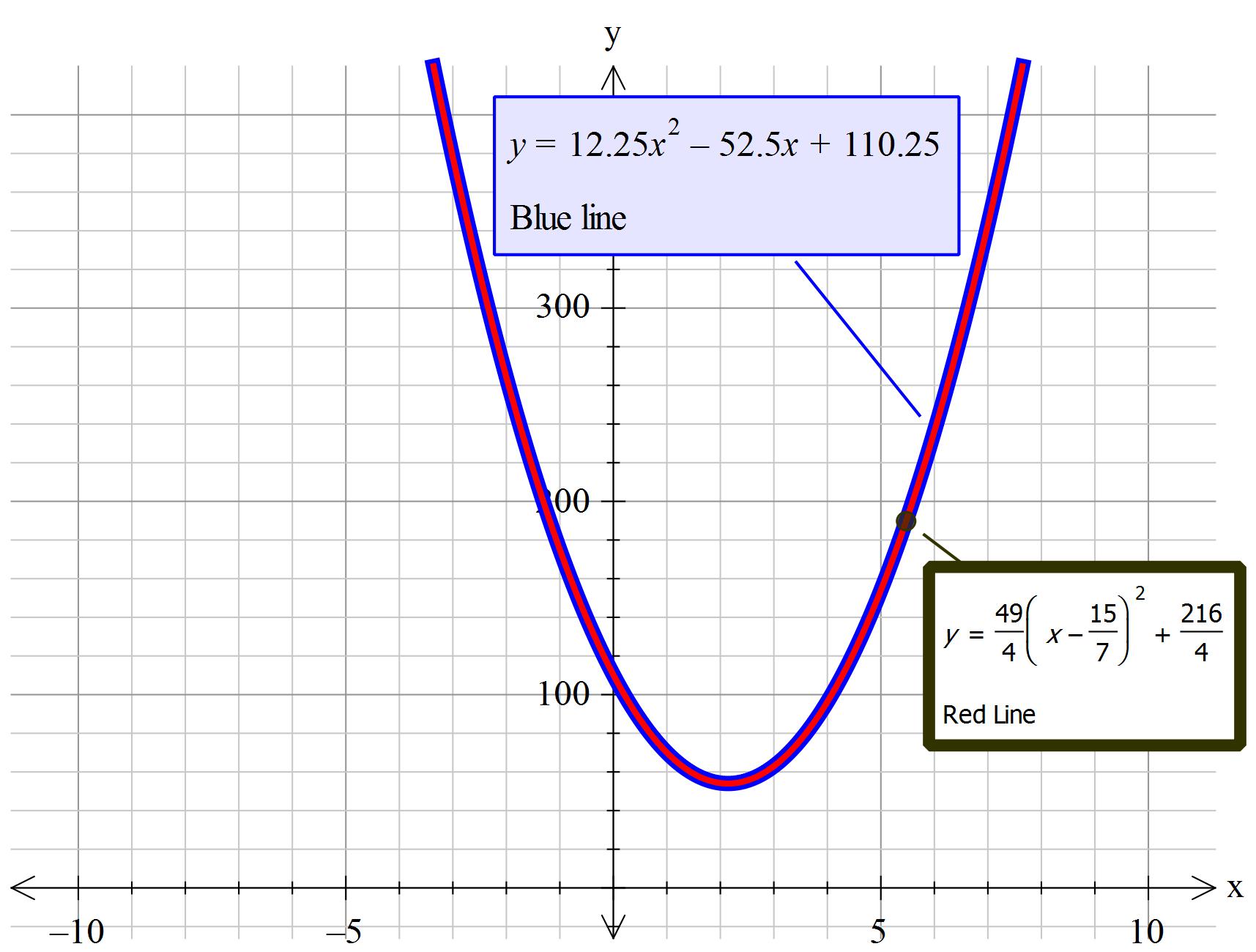
Given:
#color(green)(y=12.25x^2-52.5x+110.25)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~
Write as:
#color(blue)(" "y=49/4x^2 -105/2x+ 441/4)#
#color(brown)("Factor out "49/4)#
#color(blue)(" "y=49/4(x^2- 30/7x) +441/4)#
#color(brown)("Consider just the right hand side")#
#color(brown)(Apply "1/2xx-30/7x = -15/7x)#
# color(blue)(" "49/4(x^2- 15/7x) +441/4)#
#color(brown)("Remove the "x" from " -15/7x)#
# color(blue)(" "49/4(x^2- 15/7) +441/4)#
#color(brown)("Move the index of 2 from "x^2" to outside the bracket")#
# color(blue)(" "49/4(x- 15/7)^2 +441/4)#
#color(brown)("Now add the correction that compensates for the error we")#
#color(brown)("introduced by changing the brackets content.")#
#color(brown)("Let "k" be a constant")#
# color(blue)(" "y=49/4(x- 15/7)^2 +441/4+ k#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider the #-15/7# from inside the brackets
Then #(-15/7)^2+k=0#
#=> k = -49/4(15/7)^2 =-56 1/4=-225/4#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)(y=49/4(x- 15/7)^2 +441/4+ k#
Becomes
#color(blue)( y=49/4(x- 15/7)^2 +441/4-225/4)#
#color(blue)( y=49/4(x- 15/7)^2 +216/4)#