General vertex form is
#color(white)("XXX")y=color(green)(m)(x-color(red)a)^2+color(blue)b#
where
#color(white)("XXX")color(green)m# is a measure of the parabolic "spread";
#color(white)("XXX")color(red)a# is the #x# coordinate of the vertex; and
#color(white)("XXX")color(blue)b# is the #y# coordinate of the vertex.
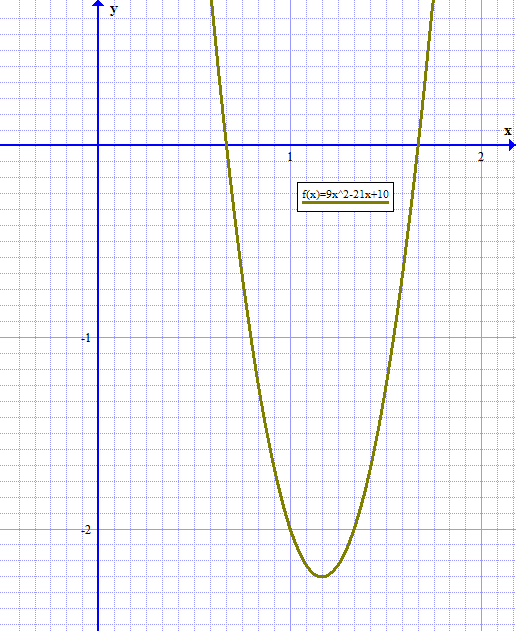
Given
#color(white)("XXX")y=9x^2-21x+10#
Extract the spread factor #color(green)m#
#color(white)("XXX")y=color(green)9(x^2-7/3x)+10#
Complete the square for the first term and subtract a corresponding amount from the second
#color(white)("XXX")y=color(green)9(x^2-7/3xcolor(magenta)(+(7/6)^2))+10color(magenta)(-9 * (7/6)^2)#
Rewrite as a squared binomial and simplify the constant
#color(white)("XXX")y=color(green)9(x-color(red)(7/6))^2+color(blue)((-9/4))#
For verification purposes, here is the graph of this function (with grid lines at #1/12# units; note: #7/6=1 2/12# and #-9/4=-2 3/12#)