Question

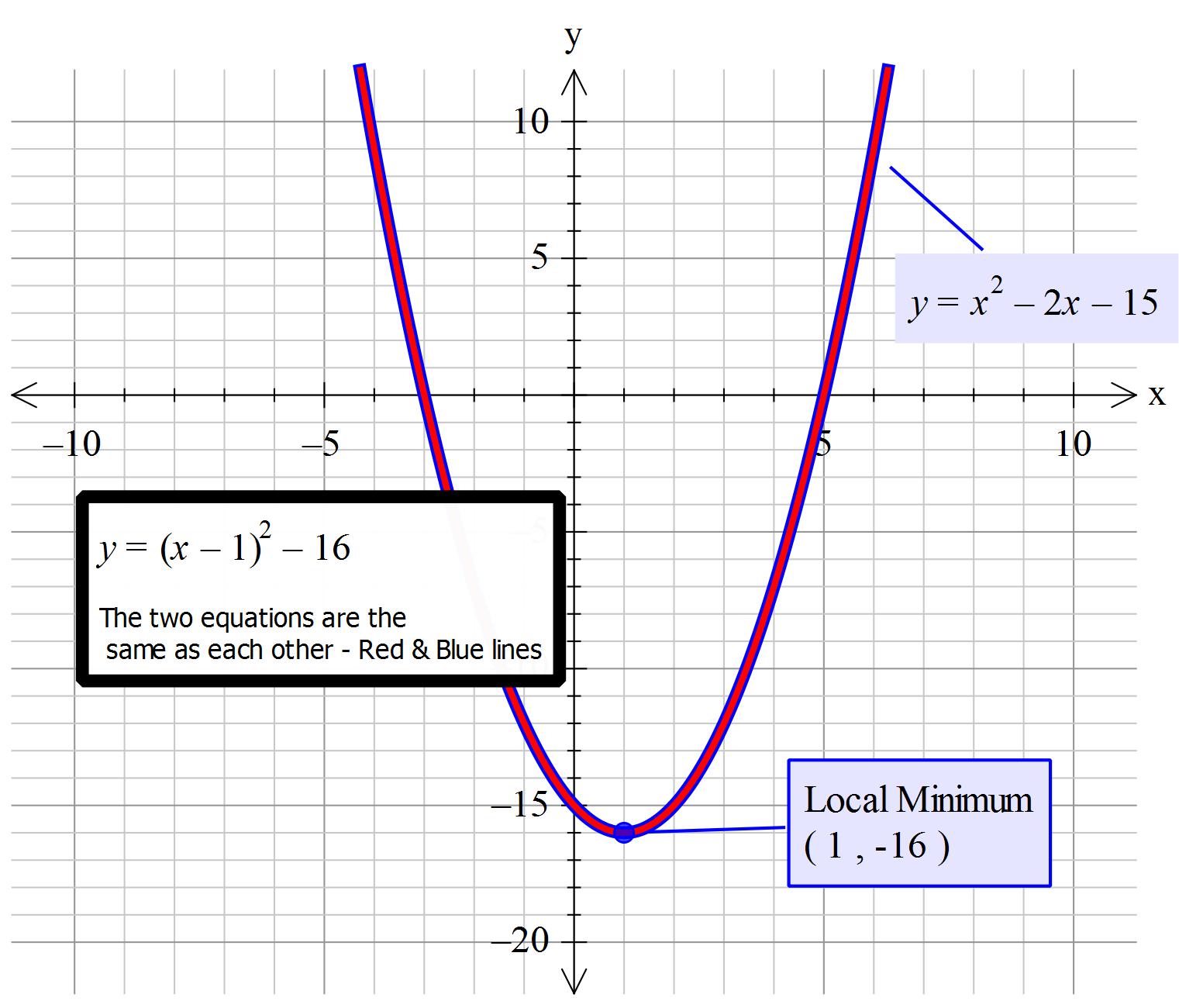
What is the vertex form of `y=x^2 - 2x - 15`?

Answer 1

`color(blue)(y=(x-1)^2-16)`

Explanation:

`color(brown)("Write as:" color(blue)(" "y=(x^2-2x)-15`

Consider only the right hand side
Remove the `x` from the `2x` inside the brackets

`color(blue)(" "(x^2-2)-15)`

Consider the constant of 2 inside the brackets

`color(brown)("Apply: "1/2xx2 = 1`

`color(blue)(" "(x^2-1)-15)`

Move the index (power) from `x^2` inside the brackets to outside the brackets

`color(blue)(" "(x-1)^2-15`

The square of the constant inside the brackets is +1. This produces an error making the equation as it stands different to when we started. So remove it by applying -1. Giving

`color(blue)(" "(x-1)^2-16`

This adjustment now means that the right hand side intrinsic value is the same as the right hand side was when we started. So at this stage we can quite correctly state that it is equal to y

`color(blue)(" "y=(x-1)^2-16)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(green)("Consider the " color(red)( -1)" inside the brackets and the "color(blue)( -16)" outside them")`

Then
`" "x_("vertex")=color(red)(-1)xx(-1) = +1`

`" "y_("vertex")=color(blue)(-16)`

So Vertex`" "->" "(x,y)" "->" "(1,-16)`

`color(blue)(y=(x-1)^2-16)`