For a more detailed explanation of method see the example of
http://socratic.org/s/asZq2L8h .Different values but the method is sound.
Given:#" "y=(x+21)(x+1)#
Let #k# be the error correcting constant
Multiply out giving
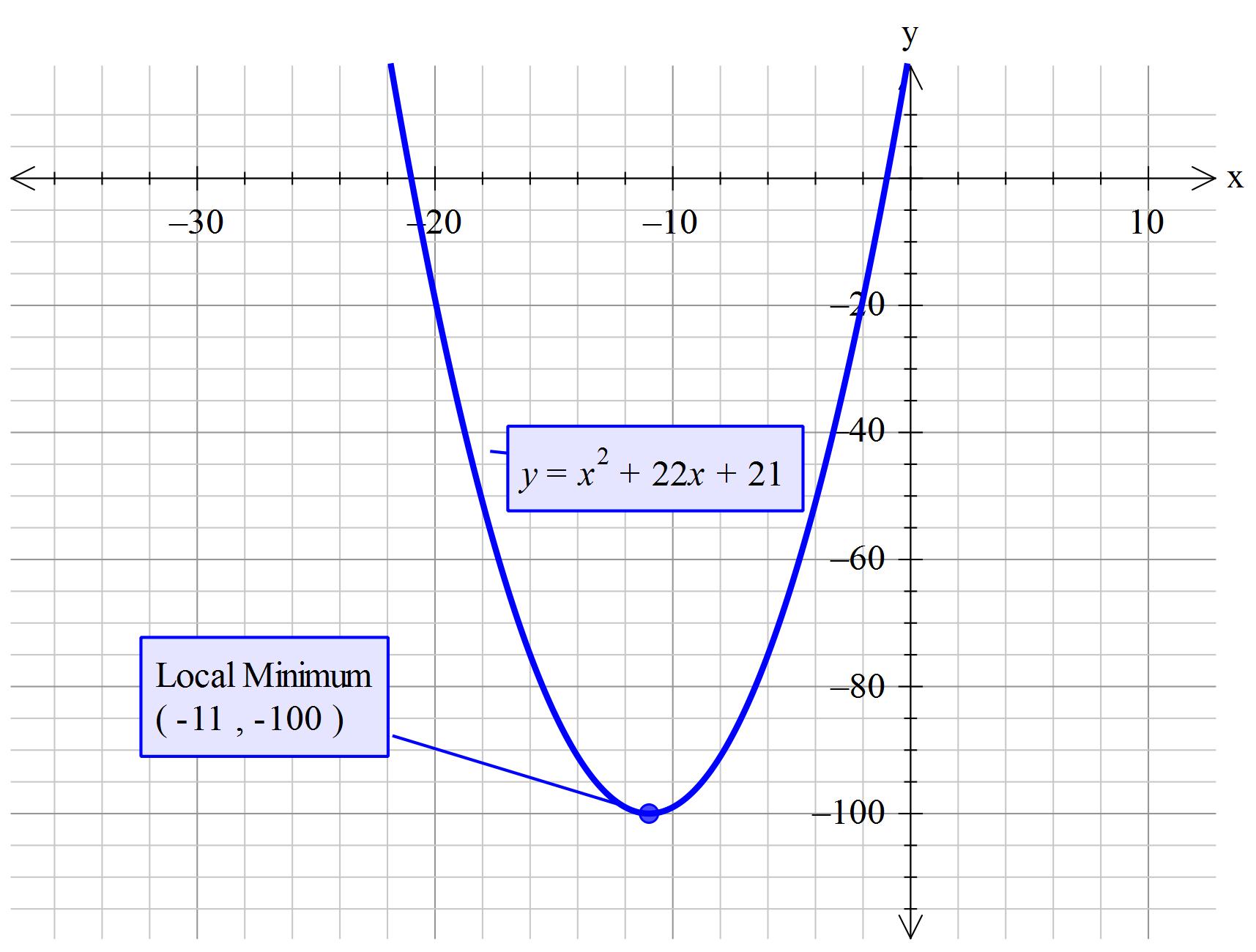
#" "y=x^2+22x+21#
#y=(x^(color(magenta)(2))+22x)+21+k" "color(brown)("No error yet so k=0 at this stage")#
Move the power to outside the bracket
#y=(x+22color(green)( x))^(color(magenta)(2)) +21+k" "color(brown)("Now we have the error "->k!=0 )#
Remove the #x# from #22color(green)(x)#
#" "y=(x+color(red)(22))^2+21+k#
Multiply #color(red)(22)" by "(1/2) =color(blue)(11 )#
#" "color(green)(y=(x+color(red)(22))^2+21+k)#
#"changes to "color(green)(y=(x+color(blue)(11))^2+21+k)#
The error introduced is #(axxb/2)^2 ->(1xx22/2)^2 =+ 121#
So #k = -121# to 'get rid' of the error
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So
#" "color (magenta)( y=(x+color(blue)(11))^2+21)-121#
#" "y=(x+11)^2-100#
#" "color(blue)("Vertex "-> (x,y)->(-11,-100)#