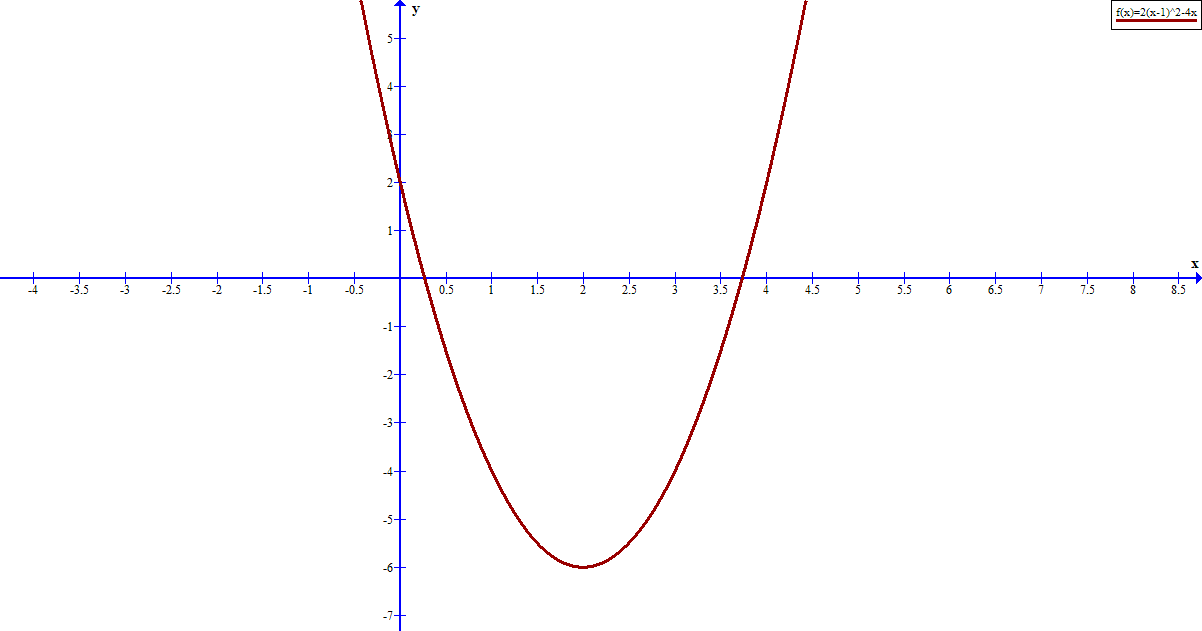
Method 1: convert the equation into vertex form
Note: vertex form is #y=color(green)m(x-color(red)a)^2+color(blue)b# for a parabola with vertex at #(color(red)a,color(blue)b)#
#y=2(x-1)^2-4xcolor(white)("xxxxxxxx")#...as given
expanding
#y=2(x^2-2x+1)-4x#
#y=2(x^2-2x+1-2x)#
#y=2(x^2-4x+1)#
completing the square
#y=2(x^2-4x+4)-6#
we added #3# to the previous #1# but this is multiplied by #2# so we need to subtract #2xx3=6# to keep this equivalent.
#y=color(green)2(x-color(red)2)^2+color(blue)(""(-6))#
which is the vertex form with vertex at #(color(red)2,color(blue)(-6))#
Method 2: Note that the slope (derivative) of the parabola at the vertex is zero
#y=2(x-1)^2-4x#
expanding:
#y=2x^2-8x+2#
at the vertex
#y'=4x-8 = 0#
#color(white)("XXX")rArr color(red)(x=2)# at the vertex
Substituting #2# for #x# back in the original equation gives
#color(blue)y=2(2-1)^2-4 * 2= 2-8color(blue)(=-6)#
Again, giving the vertex at
#color(white)("XXX")(color(red)2,color(blue)(-6))#
Method 3: Use a graphing calculator/software package