Question

What particle is needed to complete this nuclear reaction? `"_86^222Rn``->``"_84^218 Po + underline` ?

Answer 1

An alpha particle.

Explanation:

The thing to remember about nuclear equations is that mass and charge must always be conserved.

In other words, in any nuclear equation

• the overall mass number remains unchanged
• the overall atomic number remains unchanged

Your unbalanced nuclear equation looks like this

`""_ (color(white)(1)color(blue)(86))^color(darkgreen)(222)"Rn" -> ""_ (color(white)(1)color(blue)(84))^color(darkgreen)(218)"Po" + ""_ (color(blue)(Z))^color(darkgreen)(A)"?"`

The goal here is to find the atomic number, `color(blue)(Z)`, and the mass number, `color(darkgreen)(A)`, of the unknown particle.

Since the overall mass number must be conserved, you can say that

`color(darkgreen)(222) = color(darkgreen)(218) + color(darkgreen)(A) ->` conservation of mass

This will get you

`color(darkgreen)(A) = 222 - 218 = 4`

The overall atomic number is also conserved, so you can say that

`color(blue)(86) = color(blue)(84) + color(blue)(Z)`

This will get you

`color(blue)(Z) = 86 - 84 = 2`

The unknown particle has a mass number equal to `4` and an atomic number equal to `2`, which means that you're dealing with an alpha particle.

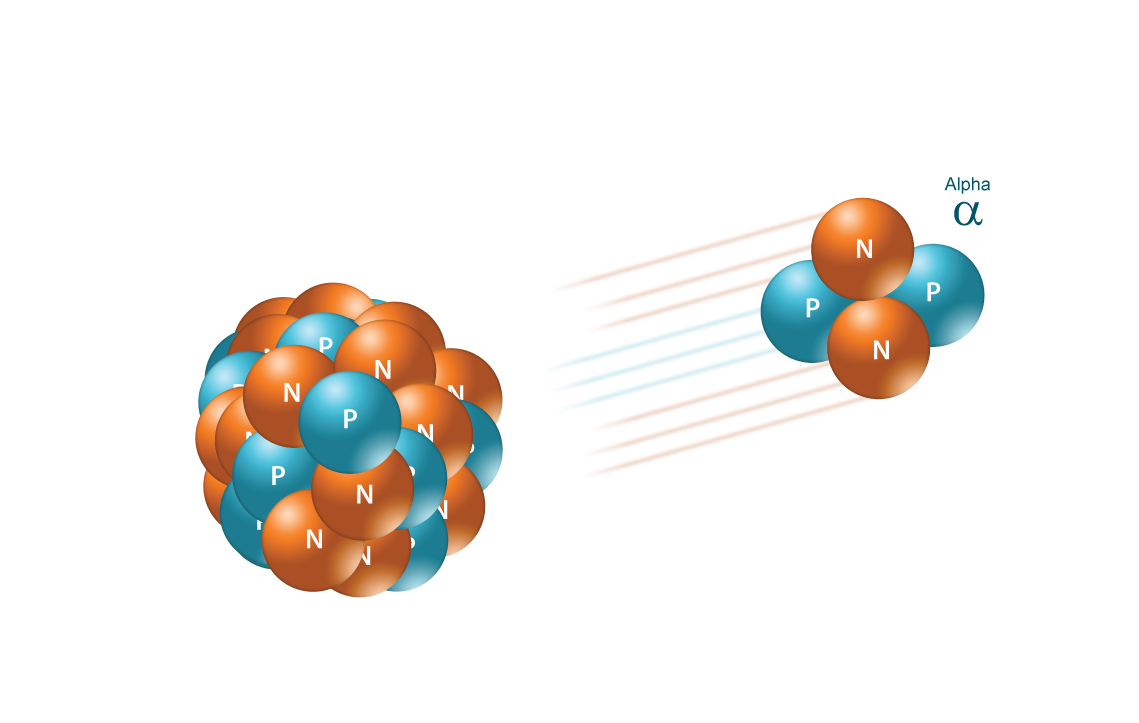
In essence, an alpha particle is simply the nucleus of a helium-4 atom, i.e. it contains `2` protons and `2` neutrons.

You can now complete the nuclear equation that describes the alpha decay of radon-222 to polonium-218

`""_ (color(white)(1)86)^222"Rn" -> ""_ (color(white)(1)84)^218"Po" + ""_ 2^4alpha`