What torque would have to be applied to a rod with a length of #5 m# and a mass of #2 kg# to change its horizontal spin by a frequency of #7 Hz# over #3 s#?
1 Answer
Jan 22, 2018
Explanation:
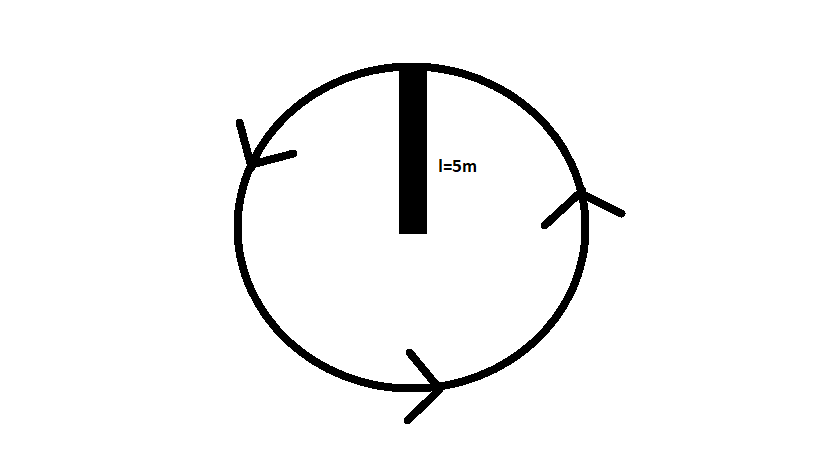
Torque is defined as the rate of change in angular momentum,
i.e
Now,moment of inertia(
so,its
Now,its rate of change in angular velocity is
So,torque acting is

