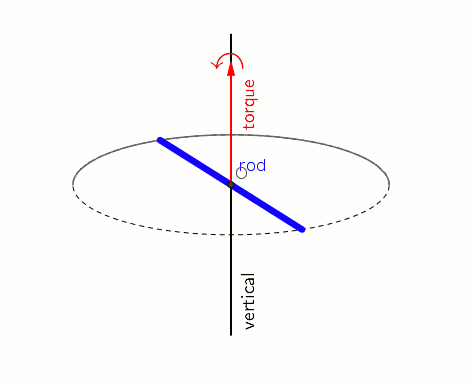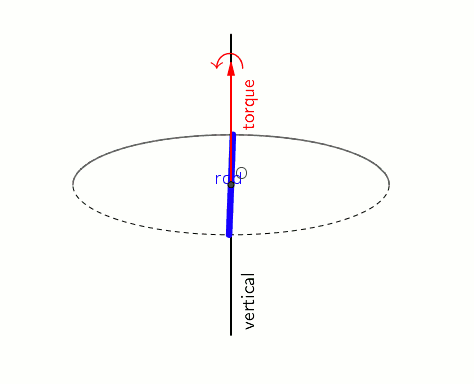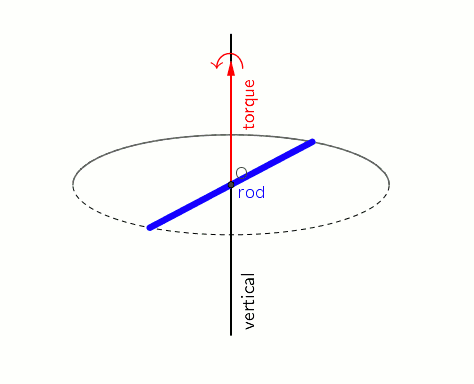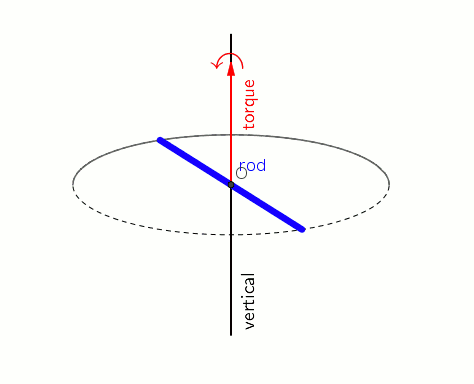
What torque would have to be applied to a rod with a length of #7 m# and a mass of #9 kg# to change its horizontal spin by a frequency #9 Hz# over #18 s#?

Question

3557 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-05T06:22:12

The torque, for the rod rotating about the center is, #=115.5Nm#
The torque, for the rod rotating about one end is, #=461.8Nm#

The torque is the rate of change of angular momentum

#tau=(dL)/dt=(d(Iomega))/dt=I(domega)/dt#

The moment of inertia of a rod, rotating about the center is

#I=1/12*mL^2#

#=1/12*9*7^2= 36.75 kgm^2#

The rate of change of angular velocity is

#(domega)/dt=(9)/18*2pi#

#=(pi) rads^(-2)#

So the torque is #tau=36.75*(pi) Nm=36.75piNm=115.5Nm#

The moment of inertia of a rod, rotating about one end is

#I=1/3*mL^2#

#=1/3*9*7^2=147kgm^2#

So,

The torque is #tau=147*(pi)=461.8Nm#

Answer 2 · 2017-04-05T07:35:03

#"Torque: "36.75pi" "N.m#

enter image source here

#"Let's apply Newton's second law for circular motion."#

#F=m*a " For linear motion"#

#T=I*alpha " For circular motion"#

#"Where T:Torque , I:Moment of Inertia , "alpha:"angular acceleration"#

#I=1/12 m* l^2"#
#"moment of inertia for a rod turning about its mass center"#
#m=9kg " , "l=7 m#

#I=1/12*9*7^2=36.75#

#alpha=(Delta omega)/(Delta t)#

#Delta omega=omega_2-omega_1#

#Delta omega=2pi(f_2-f_1)#

#f_2-f_1=9Hz#

#Delta omega=18pi#

#alpha=(18pi)/18#

#alpha=pi#

#T=36.75pi" "N*m#