Which atomic orbitals of which subshells have a dumbbell shape?
1 Answer
Well, of the simpler orbitals (i.e. not
- for the
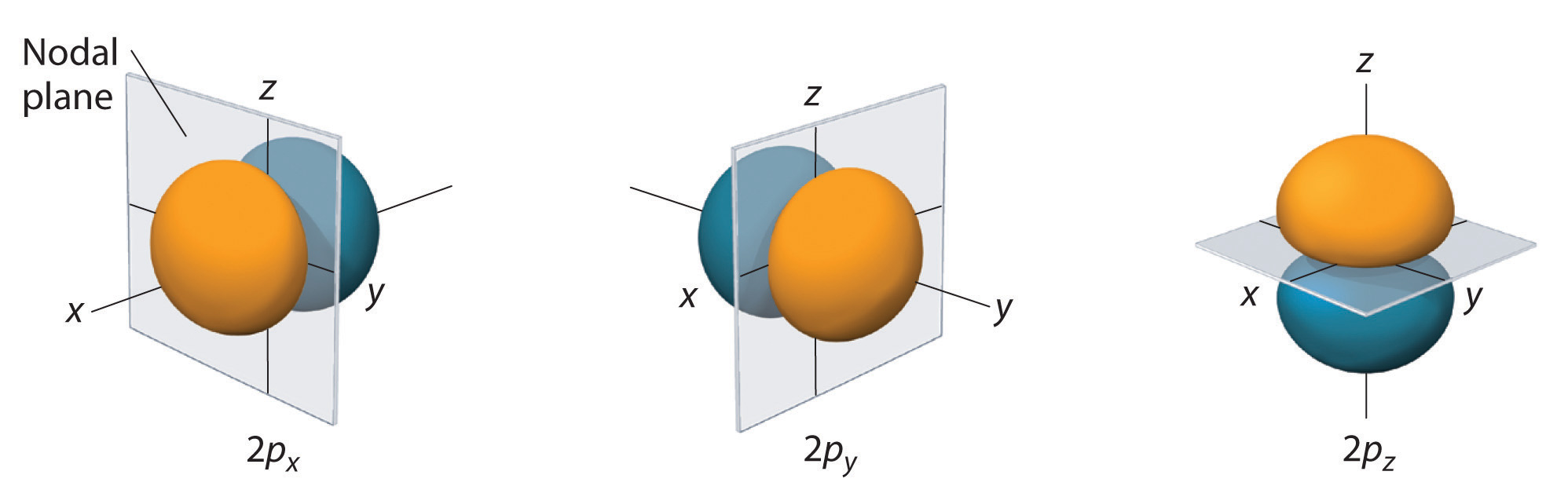
#np_x,np_y,np_z# case, one nodal plane perpendicular to the principal axis of that orbital. - for the
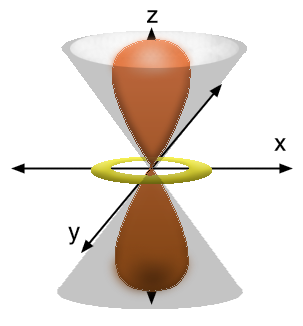
#(n-1)d_(z^2)# case, two conical nodes (each a special kind of nodal "plane").
If that doesn't make sense, that's OK. Examples that fit the bill for the above orbitals are shown below so you can see.
I go into specific mathematical proofs below (simpler than one might expect) to show why or how the above-described nodal plane or conical nodes are present.
The wave function
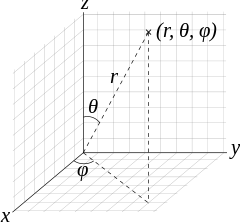
We'll focus on
When
#Y(theta,phi) = 0# for a specific plane perpendicular to the principal axis (for a nodal plane), OR#Y(theta) = 0# for two different values of#theta# (or#phi# for#Y(phi)# ) while the other angular coordinate is constant (for two conical nodes),
...we have a dumbbell shape.
Here are examples of such functions for the
#Y_(2p_x)(theta,phi) prop sinthetacosphi#
#Y_(3p_y)(theta,phi) prop sinthetasinphi#
#Y_(3d_(z^2))(theta) prop (3cos^2theta - 1)#
#Y_(2p_x)(theta,phi) = 0# when#theta = 0,pi, . . . # and/or#phi = pi/2,(3pi)/2, . . . # . By the definition of#theta# and#phi# above, that forms a node along the#z# axis and the#y# axis, giving a nodal#bb(yz)# plane for the#bb(2p_x)# orbital. Indeed, the#yz# plane is perpendicular to the principal,#bb(x)# axis.
So, the
#2p_x# orbital is dumbbell-shaped, just like the#2p_y# and#2p_z# .

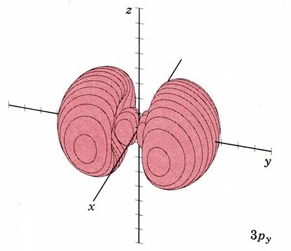
#Y_(3p_y)(theta,phi) = 0# when#theta = 0,pi, . . . # and/or#phi = 0,pi, . . . # , which marks nodes along the#z# axis for#theta = 0,pi# and the#x# axis for#phi = 0,pi# , giving us a nodal#bb(xz)# plane, which is indeed perpendicular to the principal,#bb(y)# axis.
So, the
#3p_y# orbital is dumbbell-shaped, just like the#3p_x# and#3p_z# .

#Y_(3d_(z^2))(theta) = 0# when#3cos^2theta - 1 = 0# . It turns out that solving that gives#theta = arccos(pm1/sqrt3)# , which corresponds to an axis about#bb(54.7^@)# from the#z# axis.
Since
#Y_(3d_(z^2))# is not a function of#phi# though,#phi# is constant, and the angle from the#z# axis is revolved around the#z# axis, generating the conical nodes (with a decline of#~~54.7^@# and#~~234.7^@# , respectively, from the#bb(z)# axis).One conical node is from
#theta = arccos(1/sqrt3)# , and the other is from#theta = arccos(-1/sqrt3)# .So, the
#3d_z^2# orbital is dumbbell-shaped, as shown below with the conical nodes:


